A Clustering Approach to Edge Controller Placement in Software Defined Networks with Cost Balancing

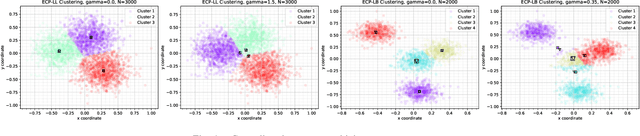
In this work we introduce two novel deterministic annealing based clustering algorithms to address the problem of Edge Controller Placement (ECP) in wireless edge networks. These networks lie at the core of the fifth generation (5G) wireless systems and beyond. These algorithms, ECP-LL and ECP-LB, address the dominant leader-less and leader-based controller placement topologies and have linear computational complexity in terms of network size, maximum number of clusters and dimensionality of data. Each algorithm tries to place controllers close to edge node clusters and not far away from other controllers to maintain a reasonable balance between synchronization and delay costs. While the ECP problem can be conveniently expressed as a multi-objective mixed integer non-linear program (MINLP), our algorithms outperform state of art MINLP solver, BARON both in terms of accuracy and speed. Our proposed algorithms have the competitive edge of avoiding poor local minima through a Shannon entropy term in the clustering objective function. Most ECP algorithms are highly susceptible to poor local minima and greatly depend on initialization.

Data Clustering and Graph Partitioning via Simulated Mixing

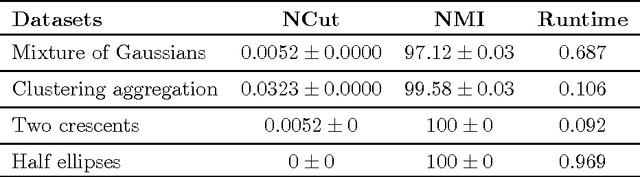
Spectral clustering approaches have led to well-accepted algorithms for finding accurate clusters in a given dataset. However, their application to large-scale datasets has been hindered by computational complexity of eigenvalue decompositions. Several algorithms have been proposed in the recent past to accelerate spectral clustering, however they compromise on the accuracy of the spectral clustering to achieve faster speed. In this paper, we propose a novel spectral clustering algorithm based on a mixing process on a graph. Unlike the existing spectral clustering algorithms, our algorithm does not require computing eigenvectors. Specifically, it finds the equivalent of a linear combination of eigenvectors of the normalized similarity matrix weighted with corresponding eigenvalues. This linear combination is then used to partition the dataset into meaningful clusters. Simulations on real datasets show that partitioning datasets based on such linear combinations of eigenvectors achieves better accuracy than standard spectral clustering methods as the number of clusters increase. Our algorithm can easily be implemented in a distributed setting.