Sequence Generation via Subsequence Similarity: Theory and Application to UAV Identification

The ability to generate synthetic sequences is crucial for a wide range of applications, and recent advances in deep learning architectures and generative frameworks have greatly facilitated this process. Particularly, unconditional one-shot generative models constitute an attractive line of research that focuses on capturing the internal information of a single image, video, etc. to generate samples with similar contents. Since many of those one-shot models are shifting toward efficient non-deep and non-adversarial approaches, we examine the versatility of a one-shot generative model for augmenting whole datasets. In this work, we focus on how similarity at the subsequence level affects similarity at the sequence level, and derive bounds on the optimal transport of real and generated sequences based on that of corresponding subsequences. We use a one-shot generative model to sample from the vicinity of individual sequences and generate subsequence-similar ones and demonstrate the improvement of this approach by applying it to the problem of Unmanned Aerial Vehicle (UAV) identification using limited radio-frequency (RF) signals. In the context of UAV identification, RF fingerprinting is an effective method for distinguishing legitimate devices from malicious ones, but heterogenous environments and channel impairments can impose data scarcity and affect the performance of classification models. By using subsequence similarity to augment sequences of RF data with a low ratio (5\%-20\%) of training dataset, we achieve significant improvements in performance metrics such as accuracy, precision, recall, and F1 score.

Orthogonal Non-negative Matrix Factorization: a Maximum-Entropy-Principle Approach

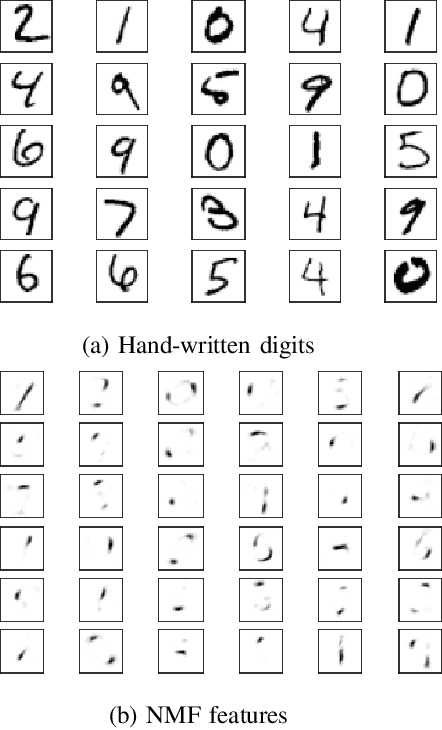
In this paper, we introduce a new methodology to solve the orthogonal non-negative matrix factorization (ONMF) problem, where the objective is to approximate an input data matrix by the product of two non-negative matrices, the features matrix and the mixing matrix, while one of them is orthogonal. We show how the ONMF can be interpreted as a specific facility-location problem (FLP), and adapt a maximum-entropy-principle based solution for FLP to the ONMF problem. The proposed approach guarantees orthogonality of the features or the mixing matrix, while ensuring that both of the matrix factors are non-negative. Also, the features (mixing) matrix has exactly one non-zero element across each row (column), providing the maximum sparsity of the orthogonal factor. This enables a semantic interpretation of the underlying data matrix using non-overlapping features. The experiments on synthetic data and a standard microarray dataset demonstrate significant improvements in terms of sparsity and orthogonality scores of features (mixing) matrices, while achieving approximately the same or better (up to 3%) reconstruction errors.

A Clustering Approach to Edge Controller Placement in Software Defined Networks with Cost Balancing

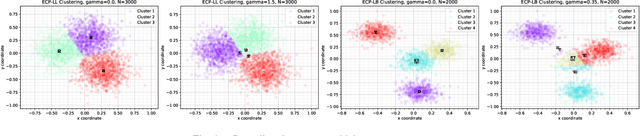
In this work we introduce two novel deterministic annealing based clustering algorithms to address the problem of Edge Controller Placement (ECP) in wireless edge networks. These networks lie at the core of the fifth generation (5G) wireless systems and beyond. These algorithms, ECP-LL and ECP-LB, address the dominant leader-less and leader-based controller placement topologies and have linear computational complexity in terms of network size, maximum number of clusters and dimensionality of data. Each algorithm tries to place controllers close to edge node clusters and not far away from other controllers to maintain a reasonable balance between synchronization and delay costs. While the ECP problem can be conveniently expressed as a multi-objective mixed integer non-linear program (MINLP), our algorithms outperform state of art MINLP solver, BARON both in terms of accuracy and speed. Our proposed algorithms have the competitive edge of avoiding poor local minima through a Shannon entropy term in the clustering objective function. Most ECP algorithms are highly susceptible to poor local minima and greatly depend on initialization.

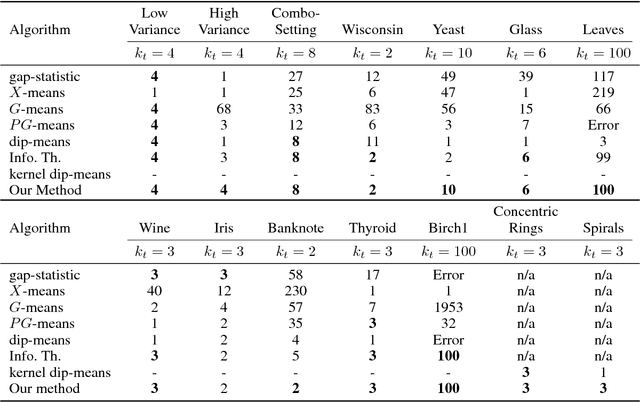
On the True Number of Clusters in a Dataset

One of the main challenges in cluster analysis is estimating the true number of clusters in a dataset. This paper quantifies a notion of persistence of a clustering solution over a range of resolution scales, which is used to characterize the natural clusters and estimate the true number of clusters in a dataset. We show that this quantification of persistence is associated with evaluating the largest eigenvalue of the underlying cluster covariance matrix. Detailed experiments on a variety of standard and synthetic datasets demonstrate that the proposed persistence-based indicator outperforms the existing approaches, such as, gap-statistic method, $X$-means, $G$-means, $PG$-means, dip-means algorithms and information-theoretic method, in accurately predicting the true number of clusters. Interestingly, our method can be explained in terms of the phase-transition phenomenon in the deterministic annealing algorithm where the number of cluster centers changes (bifurcates) with respect to an annealing parameter. However, the approach suggested in this paper is independent of the choice of clustering algorithm; and can be used in conjunction with any suitable clustering algorithm.