Sequence Generation via Subsequence Similarity: Theory and Application to UAV Identification

The ability to generate synthetic sequences is crucial for a wide range of applications, and recent advances in deep learning architectures and generative frameworks have greatly facilitated this process. Particularly, unconditional one-shot generative models constitute an attractive line of research that focuses on capturing the internal information of a single image, video, etc. to generate samples with similar contents. Since many of those one-shot models are shifting toward efficient non-deep and non-adversarial approaches, we examine the versatility of a one-shot generative model for augmenting whole datasets. In this work, we focus on how similarity at the subsequence level affects similarity at the sequence level, and derive bounds on the optimal transport of real and generated sequences based on that of corresponding subsequences. We use a one-shot generative model to sample from the vicinity of individual sequences and generate subsequence-similar ones and demonstrate the improvement of this approach by applying it to the problem of Unmanned Aerial Vehicle (UAV) identification using limited radio-frequency (RF) signals. In the context of UAV identification, RF fingerprinting is an effective method for distinguishing legitimate devices from malicious ones, but heterogenous environments and channel impairments can impose data scarcity and affect the performance of classification models. By using subsequence similarity to augment sequences of RF data with a low ratio (5\%-20\%) of training dataset, we achieve significant improvements in performance metrics such as accuracy, precision, recall, and F1 score.

Orthogonal Non-negative Matrix Factorization: a Maximum-Entropy-Principle Approach

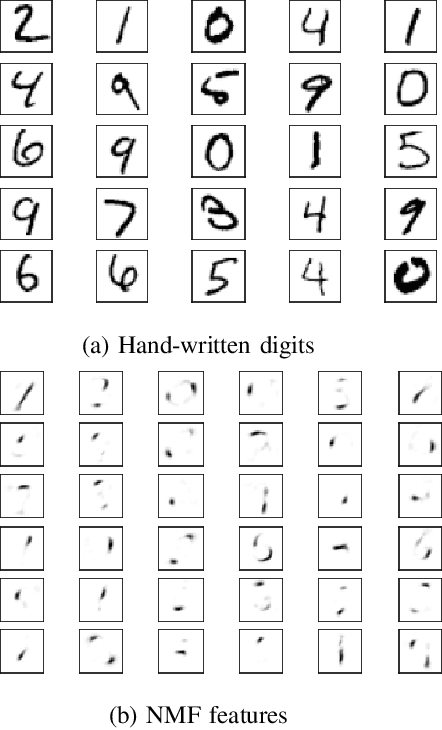
In this paper, we introduce a new methodology to solve the orthogonal non-negative matrix factorization (ONMF) problem, where the objective is to approximate an input data matrix by the product of two non-negative matrices, the features matrix and the mixing matrix, while one of them is orthogonal. We show how the ONMF can be interpreted as a specific facility-location problem (FLP), and adapt a maximum-entropy-principle based solution for FLP to the ONMF problem. The proposed approach guarantees orthogonality of the features or the mixing matrix, while ensuring that both of the matrix factors are non-negative. Also, the features (mixing) matrix has exactly one non-zero element across each row (column), providing the maximum sparsity of the orthogonal factor. This enables a semantic interpretation of the underlying data matrix using non-overlapping features. The experiments on synthetic data and a standard microarray dataset demonstrate significant improvements in terms of sparsity and orthogonality scores of features (mixing) matrices, while achieving approximately the same or better (up to 3%) reconstruction errors.