On the True Number of Clusters in a Dataset

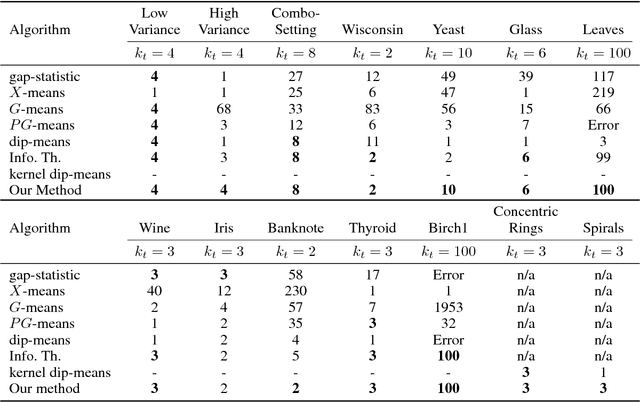
One of the main challenges in cluster analysis is estimating the true number of clusters in a dataset. This paper quantifies a notion of persistence of a clustering solution over a range of resolution scales, which is used to characterize the natural clusters and estimate the true number of clusters in a dataset. We show that this quantification of persistence is associated with evaluating the largest eigenvalue of the underlying cluster covariance matrix. Detailed experiments on a variety of standard and synthetic datasets demonstrate that the proposed persistence-based indicator outperforms the existing approaches, such as, gap-statistic method, $X$-means, $G$-means, $PG$-means, dip-means algorithms and information-theoretic method, in accurately predicting the true number of clusters. Interestingly, our method can be explained in terms of the phase-transition phenomenon in the deterministic annealing algorithm where the number of cluster centers changes (bifurcates) with respect to an annealing parameter. However, the approach suggested in this paper is independent of the choice of clustering algorithm; and can be used in conjunction with any suitable clustering algorithm.