Two Completely Parameter-Free Alternating Gradient Projection Algorithms for Nonconvex-(strongly) Concave Minimax Problems

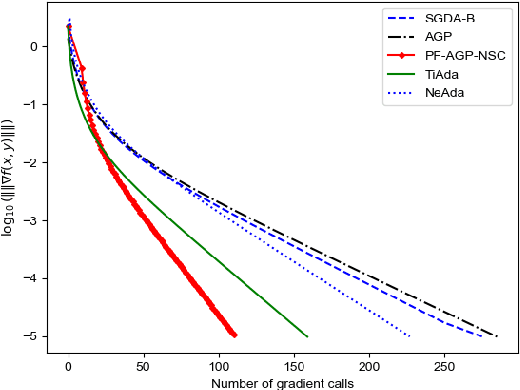
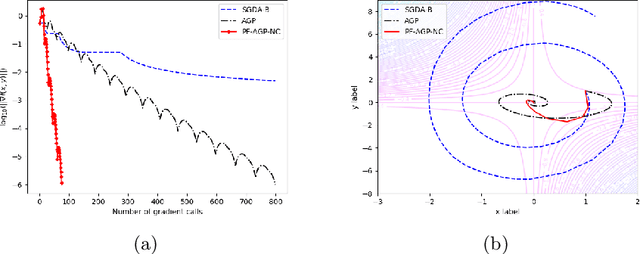
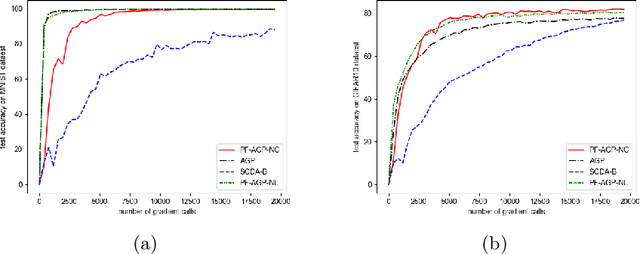
Due to their importance in various emerging applications, efficient algorithms for solving minimax problems have recently received increasing attention. However, many existing algorithms require prior knowledge of the problem parameters in order to achieve optimal iteration complexity. In this paper, we propose a completely parameter-free alternating gradient projection (PF-AGP) algorithm to solve the smooth nonconvex-(strongly) concave minimax problems using a backtracking strategy, which does not require prior knowledge of parameters such as the Lipschtiz constant $L$ or the strongly concave constant $\mu$. The PF-AGP algorithm utilizes a parameter-free gradient projection step to alternately update the outer and inner variables in each iteration. We show that the total number of gradient calls of the PF-AGP algorithm to obtain an $\varepsilon$-stationary point for nonconvex-strongly concave minimax problems is upper bounded by $\mathcal{O}\left( L\kappa^3\varepsilon^{-2} \right)$ where $\kappa$ is the condition number, while the total number of gradient calls to obtain an $\varepsilon$-stationary point for nonconvex-concave minimax problems is upper bounded by $\mathcal{O}\left( L^4\varepsilon^{-4} \right)$. As far as we know, this is the first completely parameter-free algorithm for solving nonconvex-strongly concave minimax problems, and it is also the completely parameter-free algorithm which achieves the best iteration complexity in single loop method for solving nonconvex-concave minimax problems. Numerical results validate the efficiency of the proposed PF-AGP algorithm.

A Fully Parameter-Free Second-Order Algorithm for Convex-Concave Minimax Problems with Optimal Iteration Complexity

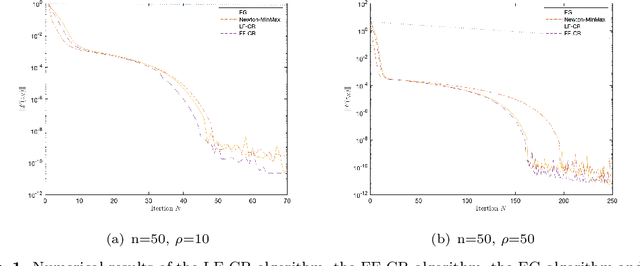
In this paper, we study second-order algorithms for the convex-concave minimax problem, which has attracted much attention in many fields such as machine learning in recent years. We propose a Lipschitz-free cubic regularization (LF-CR) algorithm for solving the convex-concave minimax optimization problem without knowing the Lipschitz constant. It can be shown that the iteration complexity of the LF-CR algorithm to obtain an $\epsilon$-optimal solution with respect to the restricted primal-dual gap is upper bounded by $\mathcal{O}(\frac{\rho\|z^0-z^*\|^3}{\epsilon})^{\frac{2}{3}}$, where $z^0=(x^0,y^0)$ is a pair of initial points, $z^*=(x^*,y^*)$ is a pair of optimal solutions, and $\rho$ is the Lipschitz constant. We further propose a fully parameter-free cubic regularization (FF-CR) algorithm that does not require any parameters of the problem, including the Lipschitz constant and the upper bound of the distance from the initial point to the optimal solution. We also prove that the iteration complexity of the FF-CR algorithm to obtain an $\epsilon$-optimal solution with respect to the gradient norm is upper bounded by $\mathcal{O}(\frac{\rho\|z^0-z^*\|^2}{\epsilon})^{\frac{2}{3}}$. Numerical experiments show the efficiency of both algorithms. To the best of our knowledge, the proposed FF-CR algorithm is the first completely parameter-free second-order algorithm for solving convex-concave minimax optimization problems, and its iteration complexity is consistent with the optimal iteration complexity lower bound of existing second-order algorithms with parameters for solving convex-concave minimax problems.