Two Completely Parameter-Free Alternating Gradient Projection Algorithms for Nonconvex-(strongly) Concave Minimax Problems

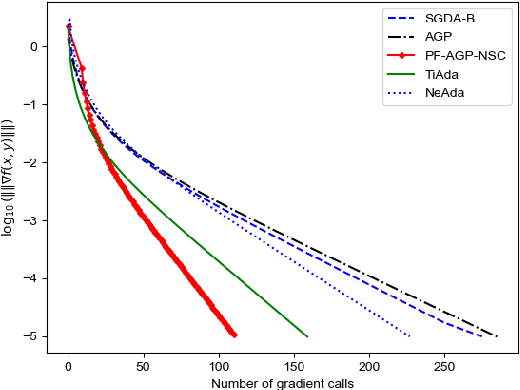
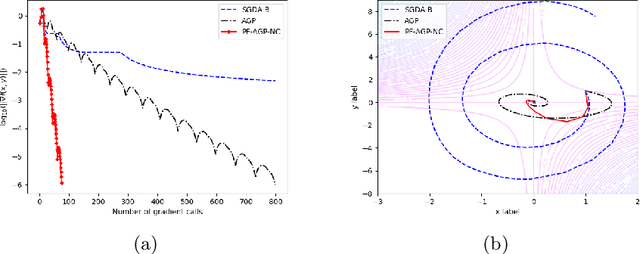
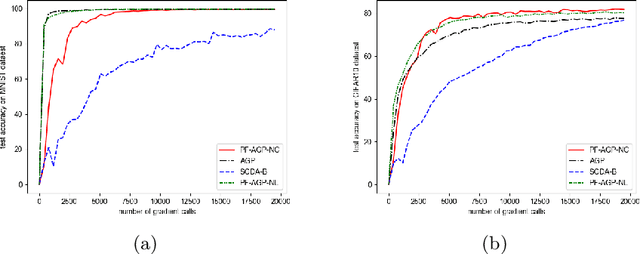
Due to their importance in various emerging applications, efficient algorithms for solving minimax problems have recently received increasing attention. However, many existing algorithms require prior knowledge of the problem parameters in order to achieve optimal iteration complexity. In this paper, we propose a completely parameter-free alternating gradient projection (PF-AGP) algorithm to solve the smooth nonconvex-(strongly) concave minimax problems using a backtracking strategy, which does not require prior knowledge of parameters such as the Lipschtiz constant $L$ or the strongly concave constant $\mu$. The PF-AGP algorithm utilizes a parameter-free gradient projection step to alternately update the outer and inner variables in each iteration. We show that the total number of gradient calls of the PF-AGP algorithm to obtain an $\varepsilon$-stationary point for nonconvex-strongly concave minimax problems is upper bounded by $\mathcal{O}\left( L\kappa^3\varepsilon^{-2} \right)$ where $\kappa$ is the condition number, while the total number of gradient calls to obtain an $\varepsilon$-stationary point for nonconvex-concave minimax problems is upper bounded by $\mathcal{O}\left( L^4\varepsilon^{-4} \right)$. As far as we know, this is the first completely parameter-free algorithm for solving nonconvex-strongly concave minimax problems, and it is also the completely parameter-free algorithm which achieves the best iteration complexity in single loop method for solving nonconvex-concave minimax problems. Numerical results validate the efficiency of the proposed PF-AGP algorithm.