Primal Dual Alternating Proximal Gradient Algorithms for Nonsmooth Nonconvex Minimax Problems with Coupled Linear Constraints

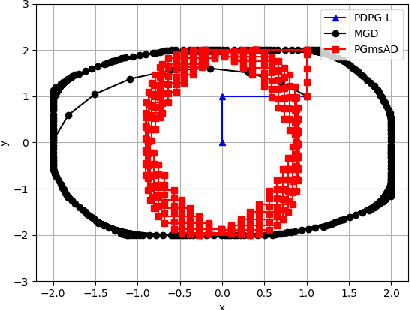
Nonconvex minimax problems have attracted wide attention in machine learning, signal processing and many other fields in recent years. In this paper, we propose a primal dual alternating proximal gradient (PDAPG) algorithm and a primal dual proximal gradient (PDPG-L) algorithm for solving nonsmooth nonconvex-strongly concave and nonconvex-linear minimax problems with coupled linear constraints, respectively. The corresponding iteration complexity of the two algorithms are proved to be $\mathcal{O}\left( \varepsilon ^{-2} \right)$ and $\mathcal{O}\left( \varepsilon ^{-3} \right)$ to reach an $\varepsilon$-stationary point, respectively. To our knowledge, they are the first two algorithms with iteration complexity guarantee for solving the two classes of minimax problems.