A Novel Negative $\ell_1$ Penalty Approach for Multiuser One-Bit Massive MIMO Downlink with PSK Signaling
Paper and Code
Oct 10, 2021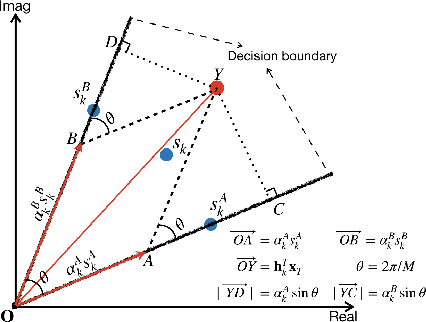
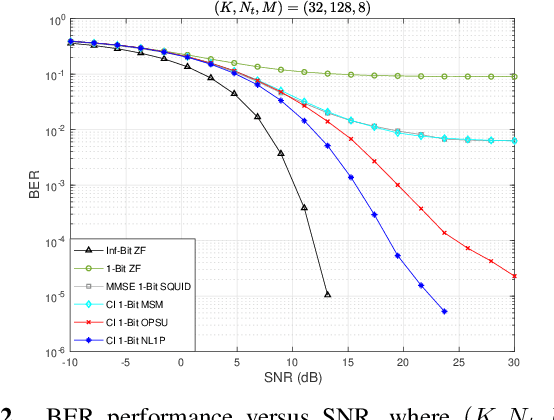

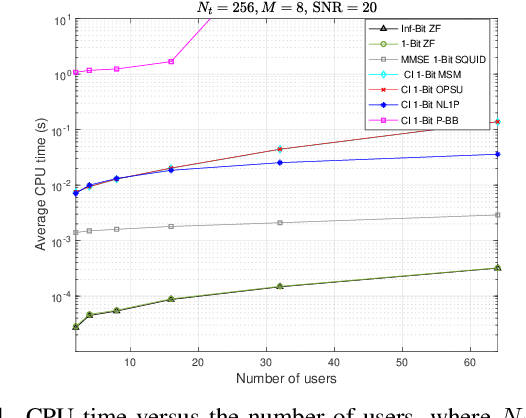
This paper considers the one-bit precoding problem for the multiuser downlink massive multiple-input multiple-output (MIMO) system with phase shift keying (PSK) modulation and focuses on the celebrated constructive interference (CI)-based problem formulation. The existence of the discrete one-bit constraint makes the problem generally hard to solve. In this paper, we propose an efficient negative $\ell_1$ penalty approach for finding a high-quality solution of the considered problem. Specifically, we first propose a novel negative $\ell_1$ penalty model, which penalizes the one-bit constraint into the objective with a negative $\ell_1$-norm term, and show the equivalence between (global and local) solutions of the original problem and the penalty problem when the penalty parameter is sufficiently large. We further transform the penalty model into an equivalent min-max problem and propose an efficient alternating optimization (AO) algorithm for solving it. The AO algorithm enjoys low per-iteration complexity and is guaranteed to converge to the stationary point of the min-max problem. Numerical results show that, compared against the state-of-the-art CI-based algorithms, the proposed algorithm generally achieves better bit-error-rate (BER) performance with lower computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge