One-Bit Sigma-Delta DFRC Waveform Design: Using Quantization Noise for Radar Probing

Dual-functional radar-communication (DFRC) signal design has received much attention lately. We consider the scenario of one-bit massive multi-input multi-output (MIMO) wherein one-bit DACs are employed for the sake of saving hardware costs. Specifically, a spatial Sigma-Delta $(\Sigma\Delta)$ modulation scheme is proposed for one-bit MIMO-DFRC waveform design. Unlike the existing approaches which require large-scale binary optimization, the proposed scheme performs $\Sigma\Delta$ modulation on a continuous-valued DFRC signal. The subsequent waveform design is formulated as a constrained least square problem, which can be efficiently solved. Moreover, we leverage quantization noise for radar probing purposes, rather than treating it as unwanted noise. Numerical results demonstrate that the proposed scheme performs well in both radar probing and downlink precoding.

Transmitting Data Through Reconfigurable Intelligent Surface: A Spatial Sigma-Delta Modulation Approach

Transmitting data using the phases on reconfigurable intelligent surfaces (RIS) is a promising solution for future energy-efficient communication systems. Recent work showed that a virtual phased massive multiuser multiple-input-multiple-out (MIMO) transmitter can be formed using only one active antenna and a large passive RIS. In this paper, we are interested in using such a system to perform MIMO downlink precoding. In this context, we may not be able to apply conventional MIMO precoding schemes, such as the simple zero-forcing (ZF) scheme, and we typically need to design the phase signals by solving optimization problems with constant modulus constraints or with discrete phase constraints, which pose challenges with high computational complexities. In this work, we propose an alternative approach based on Sigma-Delta ($\Sigma\Delta$) modulation, which is classically famous for its noise-shaping ability. Specifically, first-order $\Sigma\Delta$ modulation is applied in the spatial domain to handle phase quantization in generating constant envelope signals. Under some mild assumptions, the proposed phased $\Sigma\Delta$ modulator allows us to use the ZF scheme to synthesize the RIS reflection phases with negligible complexity. The proposed approach is empirically shown to achieve comparable bit error rate performance to the unquantized ZF scheme.

Spatial Sigma-Delta Modulation for Coarsely Quantized Massive MIMO Downlink: Flexible Designs by Convex Optimization

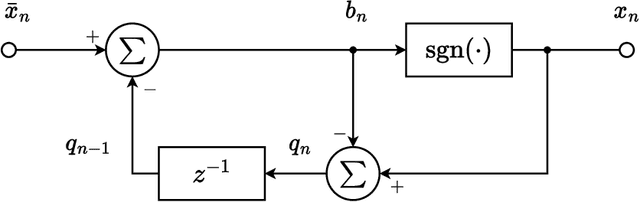
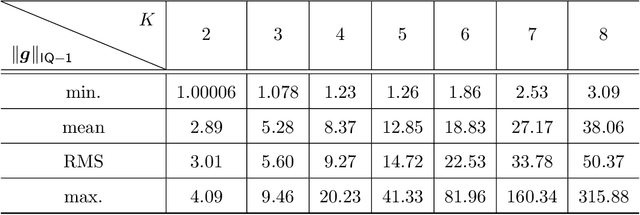
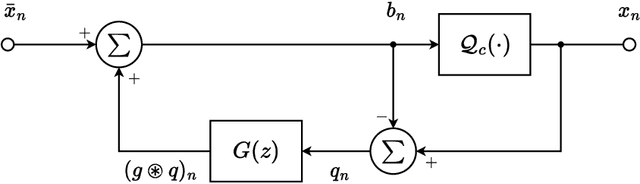
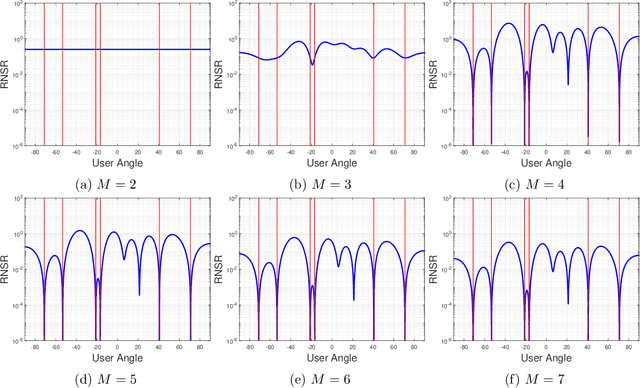
This paper considers the context of multiuser massive MIMO downlink precoding with low-resolution digital-to-analog converters (DACs) at the transmitter. This subject is motivated by the consideration that it is expensive to employ high-resolution DACs for practical massive MIMO implementations. The challenge with using low-resolution DACs is to overcome the detrimental quantization error effects. Recently, spatial Sigma-Delta modulation has arisen as a viable way to put quantization errors under control. This approach takes insight from temporal Sigma-Delta modulation in classical DAC studies. Assuming a 1D uniform linear transmit antenna array, the principle is to shape the quantization errors in space such that the shaped quantization errors are pushed away from the user-serving angle sector. In the previous studies, spatial Sigma-Delta modulation was performed by direct application of the basic first- and second-order modulators from the Sigma-Delta literature. In this paper, we develop a general Sigma-Delta modulator design framework for any given order, for any given number of quantization levels, and for any given angle sector. We formulate our design as a problem of maximizing the signal-to-quantization-and-noise ratios experienced by the users. The formulated problem is convex and can be efficiently solved by available solvers. Our proposed framework offers the alternative option of focused quantization error suppression in accordance with channel state information. Our framework can also be extended to 2D planar transmit antenna arrays. We perform numerical study under different operating conditions, and the numerical results suggest that, given a moderate number of quantization levels, say, 5 to 7 levels, our optimization-based Sigma-Delta modulation schemes can lead to bit error rate performance close to that of the unquantized counterpart.