Multilayer Simplex-structured Matrix Factorization for Hyperspectral Unmixing with Endmember Variability

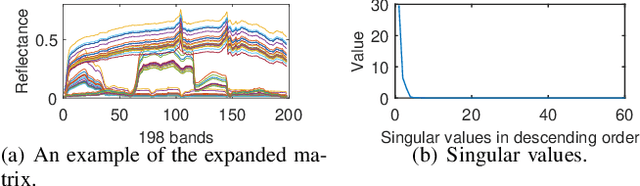
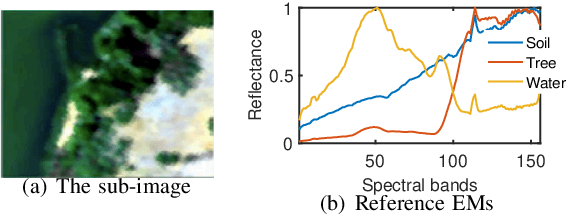
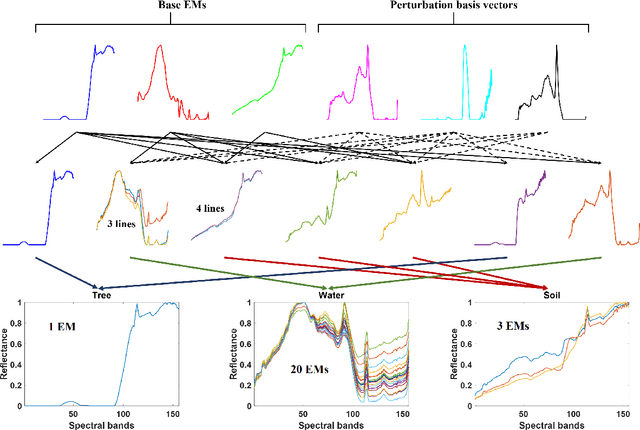
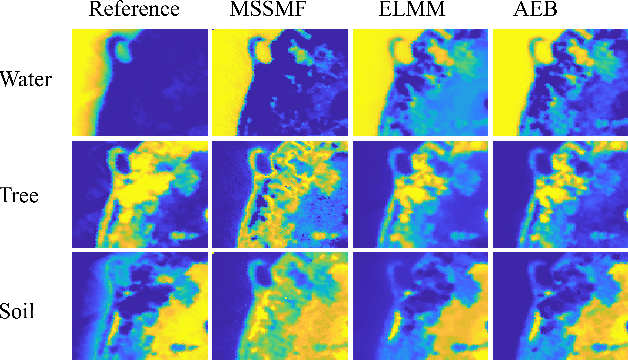
Given a hyperspectral image, the problem of hyperspectral unmixing (HU) is to identify the endmembers (or materials) and the abundance (or endmembers' contributions on pixels) that underlie the image. HU can be seen as a matrix factorization problem with a simplex structure in the abundance matrix factor. In practice, hyperspectral images may exhibit endmember variability (EV) effects -- the endmember matrix factor varies from one pixel to another. In this paper we consider a multilayer simplex-structured matrix factorization model to account for the EV effects. Our multilayer model is based on the postulate that if we arrange the varied endmembers as an expanded endmember matrix, that matrix exhibits a low-rank structure. A variational inference-based maximum-likelihood estimation method is employed to tackle the multilayer factorization problem. Simulation results are provided to demonstrate the performance of our multilayer factorization method.