User-Driven Voice Generation and Editing through Latent Space Navigation

This paper presents a user-driven approach for synthesizing highly specific target voices based on user feedback, which is particularly beneficial for speech-impaired individuals who wish to recreate their lost voices but lack prior recordings. Specifically, we leverage the neural analysis and synthesis framework to construct a low-dimensional, yet sufficiently expressive latent speaker embedding space. Within this latent space, we implement a search algorithm that guides users to their desired voice through completing a sequence of straightforward comparison tasks. Both synthetic simulations and real-world user studies demonstrate that the proposed approach can effectively approximate target voices. Moreover, by analyzing the mel-spectrogram generator's Jacobians, we identify a set of meaningful voice editing directions within the latent space. These directions enable users to further fine-tune specific attributes of the generated voice, including the pitch level, pitch range, volume, vocal tension, nasality, and tone color. Audio samples are available at https://myspeechprojects.github.io/voicedesign/.

Hyperspectral Unmixing Under Endmember Variability: A Variational Inference Framework

This work proposes a variational inference (VI) framework for hyperspectral unmixing in the presence of endmember variability (HU-EV). An EV-accounted noisy linear mixture model (LMM) is considered, and the presence of outliers is also incorporated into the model. Following the marginalized maximum likelihood (MML) principle, a VI algorithmic structure is designed for probabilistic inference for HU-EV. Specifically, a patch-wise static endmember assumption is employed to exploit spatial smoothness and to try to overcome the ill-posed nature of the HU-EV problem. The design facilitates lightweight, continuous optimization-based updates under a variety of endmember priors. Some of the priors, such as the Beta prior, were previously used under computationally heavy, sampling-based probabilistic HU-EV methods. The effectiveness of the proposed framework is demonstrated through synthetic, semi-real, and real-data experiments.

Extreme Point Pursuit -- Part I: A Framework for Constant Modulus Optimization

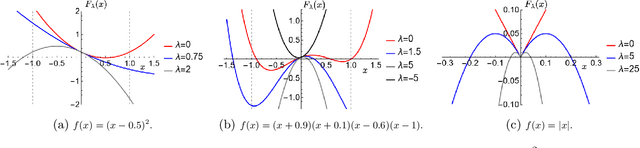
This study develops a framework for a class of constant modulus (CM) optimization problems, which covers binary constraints, discrete phase constraints, semi-orthogonal matrix constraints, non-negative semi-orthogonal matrix constraints, and several types of binary assignment constraints. Capitalizing on the basic principles of concave minimization and error bounds, we study a convex-constrained penalized formulation for general CM problems. The advantage of such formulation is that it allows us to leverage non-convex optimization techniques, such as the simple projected gradient method, to build algorithms. As the first part of this study, we explore the theory of this framework. We study conditions under which the formulation provides exact penalization results. We also examine computational aspects relating to the use of the projected gradient method for each type of CM constraint. Our study suggests that the proposed framework has a broad scope of applicability.

Extreme Point Pursuit -- Part II: Further Error Bound Analysis and Applications

In the first part of this study, a convex-constrained penalized formulation was studied for a class of constant modulus (CM) problems. In particular, the error bound techniques were shown to play a vital role in providing exact penalization results. In this second part of the study, we continue our error bound analysis for the cases of partial permutation matrices, size-constrained assignment matrices and non-negative semi-orthogonal matrices. We develop new error bounds and penalized formulations for these three cases, and the new formulations possess good structures for building computationally efficient algorithms. Moreover, we provide numerical results to demonstrate our framework in a variety of applications such as the densest k-subgraph problem, graph matching, size-constrained clustering, non-negative orthogonal matrix factorization and sparse fair principal component analysis.

Multilayer Simplex-structured Matrix Factorization for Hyperspectral Unmixing with Endmember Variability

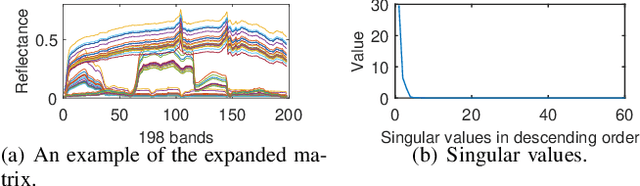
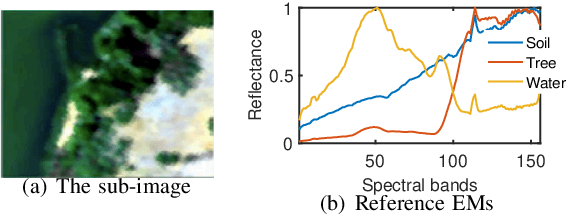
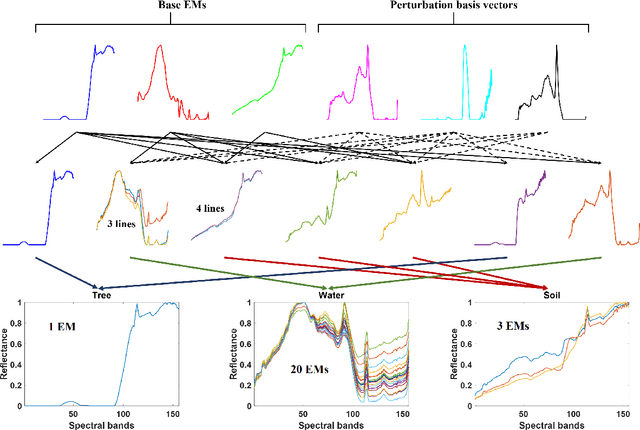
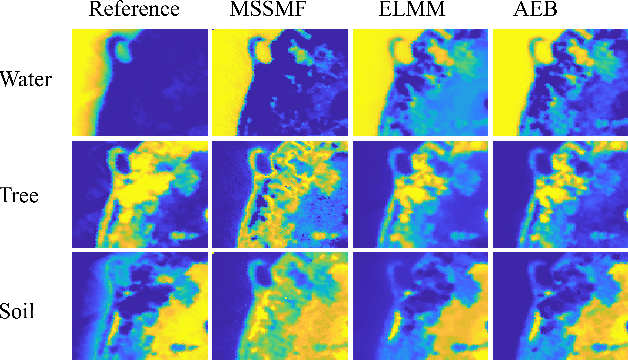
Given a hyperspectral image, the problem of hyperspectral unmixing (HU) is to identify the endmembers (or materials) and the abundance (or endmembers' contributions on pixels) that underlie the image. HU can be seen as a matrix factorization problem with a simplex structure in the abundance matrix factor. In practice, hyperspectral images may exhibit endmember variability (EV) effects -- the endmember matrix factor varies from one pixel to another. In this paper we consider a multilayer simplex-structured matrix factorization model to account for the EV effects. Our multilayer model is based on the postulate that if we arrange the varied endmembers as an expanded endmember matrix, that matrix exhibits a low-rank structure. A variational inference-based maximum-likelihood estimation method is employed to tackle the multilayer factorization problem. Simulation results are provided to demonstrate the performance of our multilayer factorization method.

Accelerated and Deep Expectation Maximization for One-Bit MIMO-OFDM Detection

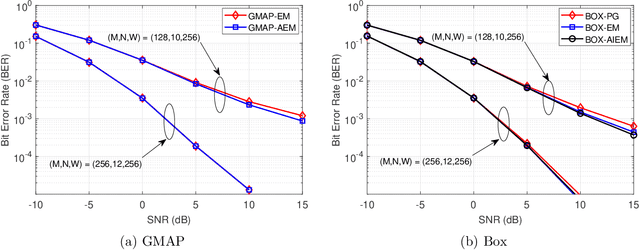
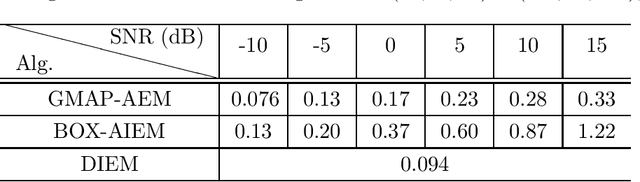
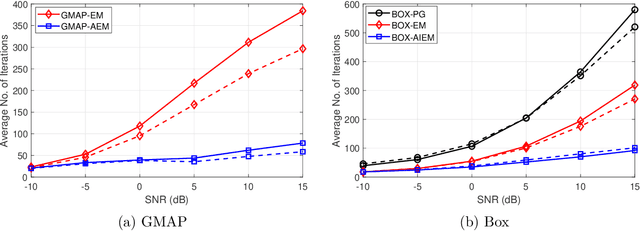
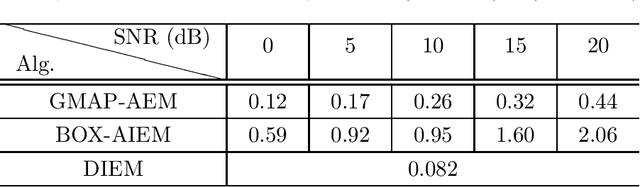
In this paper we study the expectation maximization (EM) technique for one-bit MIMO-OFDM detection (OMOD). Arising from the recent interest in massive MIMO with one-bit analog-to-digital converters, OMOD is a massive-scale problem. EM is an iterative method that can exploit the OFDM structure to process the problem in a per-iteration efficient fashion. In this study we analyze the convergence rate of EM for a class of approximate maximum-likelihood OMOD formulations, or, in a broader sense, a class of problems involving regression from quantized data. We show how the SNR and channel conditions can have an impact on the convergence rate. We do so by making a connection between the EM and the proximal gradient methods in the context of OMOD. This connection also gives us insight to build new accelerated and/or inexact EM schemes. The accelerated scheme has faster convergence in theory, and the inexact scheme provides us with the flexibility to implement EM more efficiently, with convergence guarantee. Furthermore we develop a deep EM algorithm, wherein we take the structure of our inexact EM algorithm and apply deep unfolding to train an efficient structured deep net. Simulation results show that our accelerated exact/inexact EM algorithms run much faster than their standard EM counterparts, and that the deep EM algorithm gives promising detection and runtime performances.