On decomposability and subdifferential of the tensor nuclear norm

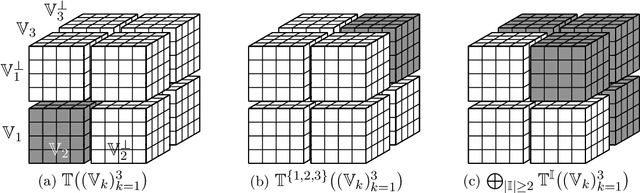
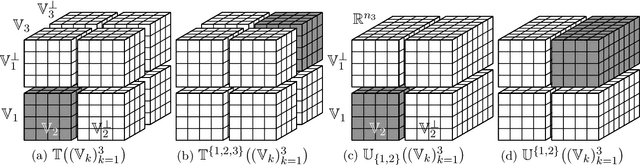
We study the decomposability and the subdifferential of the tensor nuclear norm. Both concepts are well understood and widely applied in matrices but remain unclear for higher-order tensors. We show that the tensor nuclear norm admits a full decomposability over specific subspaces and determine the largest possible subspaces that allow the full decomposability. We derive novel inclusions of the subdifferential of the tensor nuclear norm and study its subgradients in a variety of subspaces of interest. All the results hold for tensors of an arbitrary order. As an immediate application, we establish the statistical performance of the tensor robust principal component analysis, the first such result for tensors of an arbitrary order.

$\ell_1$-norm rank-one symmetric matrix factorization has no spurious second-order stationary points

This paper studies the nonsmooth optimization landscape of the $\ell_1$-norm rank-one symmetric matrix factorization problem using tools from second-order variational analysis. Specifically, as the main finding of this paper, we show that any second-order stationary point (and thus local minimizer) of the problem is actually globally optimal. Besides, some other results concerning the landscape of the problem, such as a complete characterization of the set of stationary points, are also developed, which should be interesting in their own rights. Furthermore, with the above theories, we revisit existing results on the generic minimizing behavior of simple algorithms for nonsmooth optimization and showcase the potential risk of their applications to our problem through several examples. Our techniques can potentially be applied to analyze the optimization landscapes of a variety of other more sophisticated nonsmooth learning problems, such as robust low-rank matrix recovery.

On subdifferential chain rule of matrix factorization and beyond

In this paper, we study equality-type Clarke subdifferential chain rules of matrix factorization and factorization machine. Specifically, we show for these problems that provided the latent dimension is larger than some multiple of the problem size (i.e., slightly overparameterized) and the loss function is locally Lipschitz, the subdifferential chain rules hold everywhere. In addition, we examine the tightness of the analysis through some interesting constructions and make some important observations from the perspective of optimization; e.g., we show that for all this type of problems, computing a stationary point is trivial. Some tensor generalizations and neural extensions are also discussed, albeit they remain mostly open.