Doubly Smoothed GDA: Global Convergent Algorithm for Constrained Nonconvex-Nonconcave Minimax Optimization

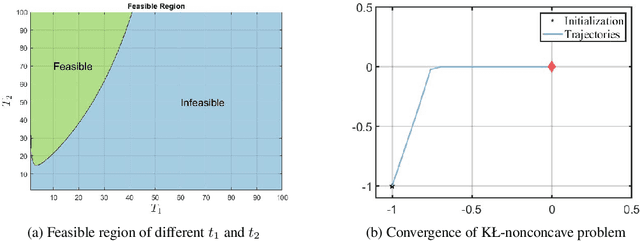
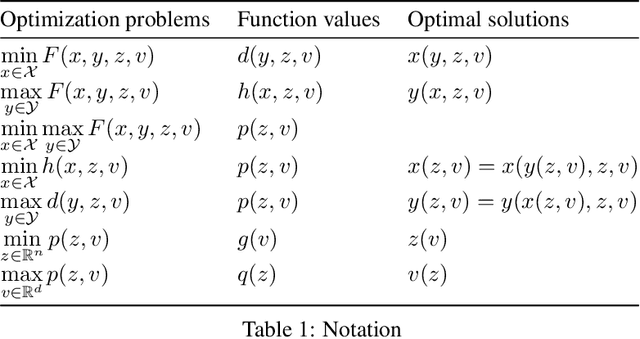
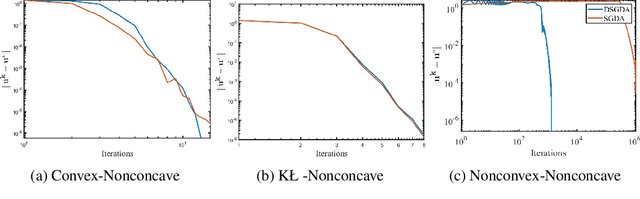
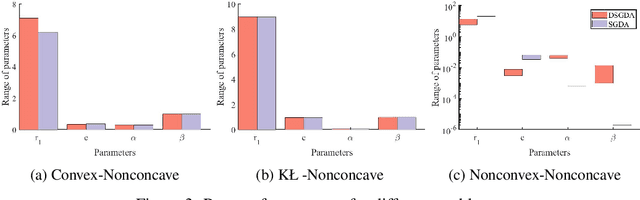
Nonconvex-nonconcave minimax optimization has been the focus of intense research over the last decade due to its broad applications in machine learning and operation research. Unfortunately, most existing algorithms cannot be guaranteed to converge and always suffer from limit cycles. Their global convergence relies on certain conditions that are difficult to check, including but not limited to the global Polyak-\L{}ojasiewicz condition, the existence of a solution satisfying the weak Minty variational inequality and $\alpha$-interaction dominant condition. In this paper, we develop the first provably convergent algorithm called doubly smoothed gradient descent ascent method, which gets rid of the limit cycle without requiring any additional conditions. We further show that the algorithm has an iteration complexity of $\mathcal{O}(\epsilon^{-4})$ for finding a game stationary point, which matches the best iteration complexity of single-loop algorithms under nonconcave-concave settings. The algorithm presented here opens up a new path for designing provable algorithms for nonconvex-nonconcave minimax optimization problems.

A Linearly Convergent Algorithm for Rotationally Invariant $\ell_1$-Norm Principal Component Analysis

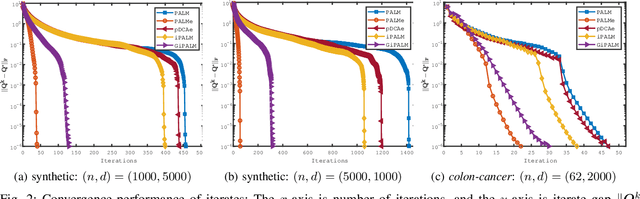
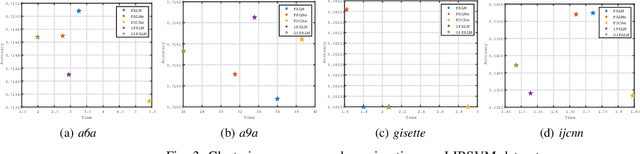
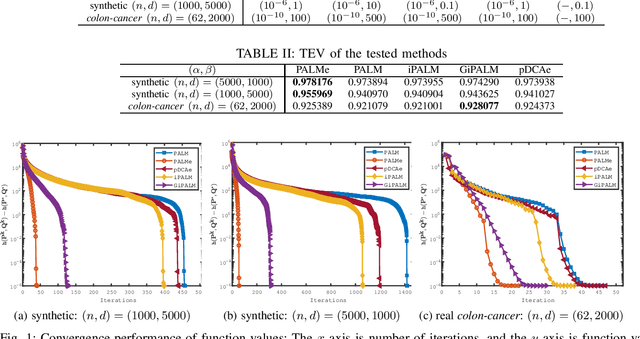
To do dimensionality reduction on the datasets with outliers, the $\ell_1$-norm principal component analysis (L1-PCA) as a typical robust alternative of the conventional PCA has enjoyed great popularity over the past years. In this work, we consider a rotationally invariant L1-PCA, which is hardly studied in the literature. To tackle it, we propose a proximal alternating linearized minimization method with a nonlinear extrapolation for solving its two-block reformulation. Moreover, we show that the proposed method converges at least linearly to a limiting critical point of the reformulated problem. Such a point is proved to be a critical point of the original problem under a condition imposed on the step size. Finally, we conduct numerical experiments on both synthetic and real datasets to support our theoretical developments and demonstrate the efficacy of our approach.