A Linearly Convergent Algorithm for Rotationally Invariant $\ell_1$-Norm Principal Component Analysis
Paper and Code
Oct 11, 2022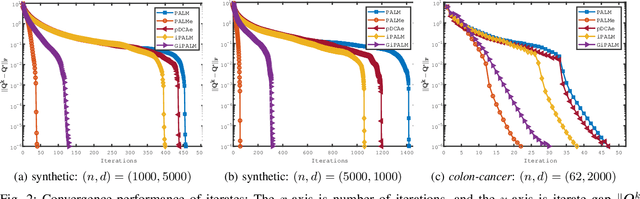
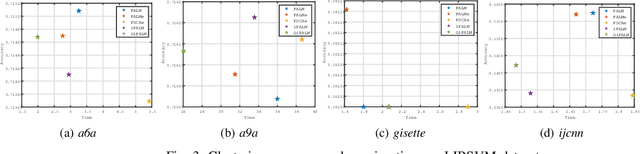

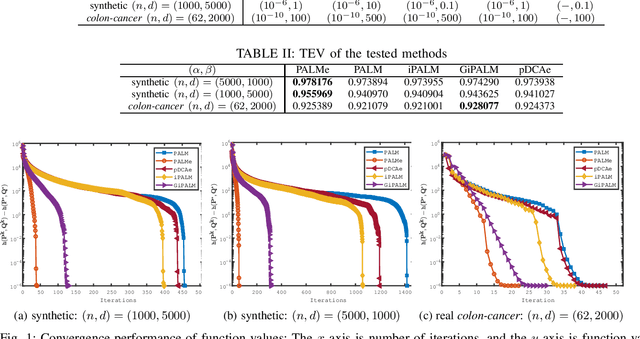
To do dimensionality reduction on the datasets with outliers, the $\ell_1$-norm principal component analysis (L1-PCA) as a typical robust alternative of the conventional PCA has enjoyed great popularity over the past years. In this work, we consider a rotationally invariant L1-PCA, which is hardly studied in the literature. To tackle it, we propose a proximal alternating linearized minimization method with a nonlinear extrapolation for solving its two-block reformulation. Moreover, we show that the proposed method converges at least linearly to a limiting critical point of the reformulated problem. Such a point is proved to be a critical point of the original problem under a condition imposed on the step size. Finally, we conduct numerical experiments on both synthetic and real datasets to support our theoretical developments and demonstrate the efficacy of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge