Privacy-Computation trade-offs in Private Repetition and Metaselection
Paper and Code
Oct 22, 2024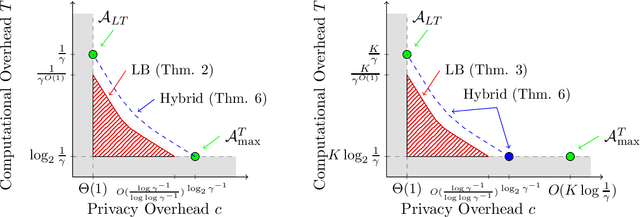
A Private Repetition algorithm takes as input a differentially private algorithm with constant success probability and boosts it to one that succeeds with high probability. These algorithms are closely related to private metaselection algorithms that compete with the best of many private algorithms, and private hyperparameter tuning algorithms that compete with the best hyperparameter settings for a private learning algorithm. Existing algorithms for these tasks pay either a large overhead in privacy cost, or a large overhead in computational cost. In this work, we show strong lower bounds for problems of this kind, showing in particular that for any algorithm that preserves the privacy cost up to a constant factor, the failure probability can only fall polynomially in the computational overhead. This is in stark contrast with the non-private setting, where the failure probability falls exponentially in the computational overhead. By carefully combining existing algorithms for metaselection, we prove computation-privacy tradeoffs that nearly match our lower bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge