Assumption-Lean Post-Integrated Inference with Negative Control Outcomes

Data integration has become increasingly common in aligning multiple heterogeneous datasets. With high-dimensional outcomes, data integration methods aim to extract low-dimensional embeddings of observations to remove unwanted variations, such as batch effects and unmeasured covariates, inherent in data collected from different sources. However, multiple hypothesis testing after data integration can be substantially biased due to the data-dependent integration processes. To address this challenge, we introduce a robust post-integrated inference (PII) method that adjusts for latent heterogeneity using negative control outcomes. By leveraging causal interpretations, we derive nonparametric identification conditions that form the basis of our PII approach. Our assumption-lean semiparametric inference method extends robustness and generality to projected direct effect estimands that account for mediators, confounders, and moderators. These estimands remain statistically meaningful under model misspecifications and with error-prone embeddings. We provide deterministic quantifications of the bias of target estimands induced by estimated embeddings and finite-sample linear expansions of the estimators with uniform concentration bounds on the residuals for all outcomes. The proposed doubly robust estimators are consistent and efficient under minimal assumptions, facilitating data-adaptive estimation with machine learning algorithms. Using random forests, we evaluate empirical statistical errors in simulations and analyze single-cell CRISPR perturbed datasets with potential unmeasured confounders.

Causal Inference for Genomic Data with Multiple Heterogeneous Outcomes

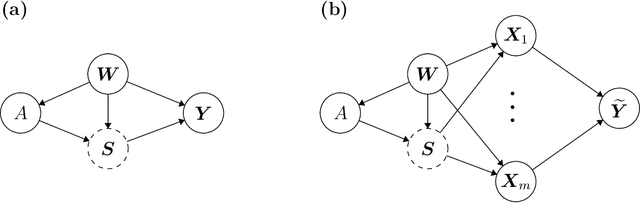
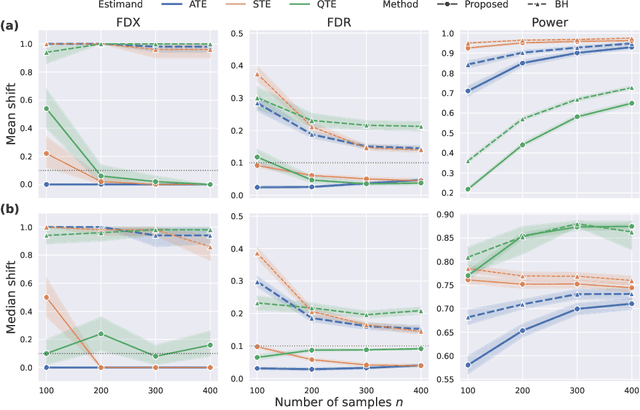
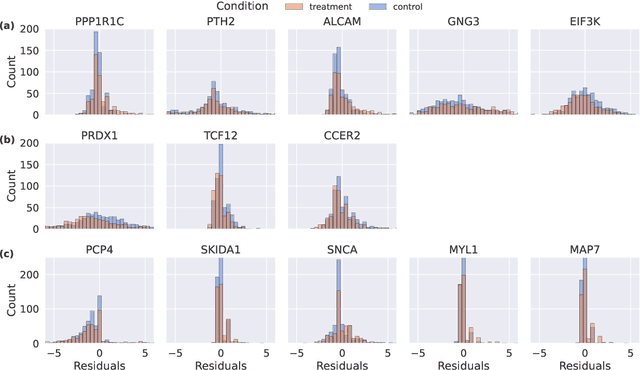
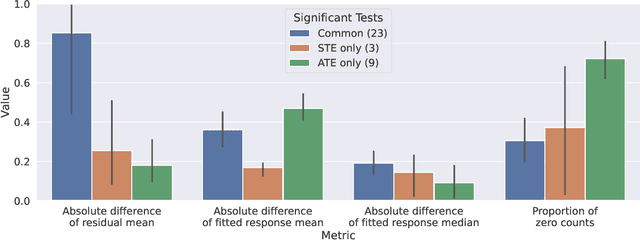
With the evolution of single-cell RNA sequencing techniques into a standard approach in genomics, it has become possible to conduct cohort-level causal inferences based on single-cell-level measurements. However, the individual gene expression levels of interest are not directly observable; instead, only repeated proxy measurements from each individual's cells are available, providing a derived outcome to estimate the underlying outcome for each of many genes. In this paper, we propose a generic semiparametric inference framework for doubly robust estimation with multiple derived outcomes, which also encompasses the usual setting of multiple outcomes when the response of each unit is available. To reliably quantify the causal effects of heterogeneous outcomes, we specialize the analysis to the standardized average treatment effects and the quantile treatment effects. Through this, we demonstrate the use of the semiparametric inferential results for doubly robust estimators derived from both Von Mises expansions and estimating equations. A multiple testing procedure based on the Gaussian multiplier bootstrap is tailored for doubly robust estimators to control the false discovery exceedance rate. Applications in single-cell CRISPR perturbation analysis and individual-level differential expression analysis demonstrate the utility of the proposed methods and offer insights into the usage of different estimands for causal inference in genomics.

Simultaneous inference for generalized linear models with unmeasured confounders

Tens of thousands of simultaneous hypothesis tests are routinely performed in genomic studies to identify differentially expressed genes. However, due to unmeasured confounders, many standard statistical approaches may be substantially biased. This paper investigates the large-scale hypothesis testing problem for multivariate generalized linear models in the presence of confounding effects. Under arbitrary confounding mechanisms, we propose a unified statistical estimation and inference framework that harnesses orthogonal structures and integrates linear projections into three key stages. It begins by disentangling marginal and uncorrelated confounding effects to recover the latent coefficients. Subsequently, latent factors and primary effects are jointly estimated through lasso-type optimization. Finally, we incorporate projected and weighted bias-correction steps for hypothesis testing. Theoretically, we establish the identification conditions of various effects and non-asymptotic error bounds. We show effective Type-I error control of asymptotic $z$-tests as sample and response sizes approach infinity. Numerical experiments demonstrate that the proposed method controls the false discovery rate by the Benjamini-Hochberg procedure and is more powerful than alternative methods. By comparing single-cell RNA-seq counts from two groups of samples, we demonstrate the suitability of adjusting confounding effects when significant covariates are absent from the model.

Extrapolated cross-validation for randomized ensembles

Ensemble methods such as bagging and random forests are ubiquitous in fields ranging from finance to genomics. However, the question of the efficient tuning of ensemble parameters has received relatively little attention. In this paper, we propose a cross-validation method, ECV (Extrapolated Cross-Validation), for tuning the ensemble and subsample sizes of randomized ensembles. Our method builds on two main ingredients: two initial estimators for small ensemble sizes using out-of-bag errors and a novel risk extrapolation technique leveraging the structure of the prediction risk decomposition. By establishing uniform consistency over ensemble and subsample sizes, we show that ECV yields $\delta$-optimal (with respect to the oracle-tuned risk) ensembles for squared prediction risk. Our theory accommodates general ensemble predictors, requires mild moment assumptions, and allows for high-dimensional regimes where the feature dimension grows with the sample size. As an illustrative example, we employ ECV to predict surface protein abundances from gene expressions in single-cell multiomics using random forests. Compared to sample-split cross-validation and K-fold cross-validation, ECV achieves higher accuracy avoiding sample splitting. Meanwhile, its computational cost is considerably lower owing to the use of the risk extrapolation technique. Further numerical results demonstrate the finite-sample accuracy of ECV for several common ensemble predictors.

The huge Package for High-dimensional Undirected Graph Estimation in R

We describe an R package named huge which provides easy-to-use functions for estimating high dimensional undirected graphs from data. This package implements recent results in the literature, including Friedman et al. (2007), Liu et al. (2009, 2012) and Liu et al. (2010). Compared with the existing graph estimation package glasso, the huge package provides extra features: (1) instead of using Fortan, it is written in C, which makes the code more portable and easier to modify; (2) besides fitting Gaussian graphical models, it also provides functions for fitting high dimensional semiparametric Gaussian copula models; (3) more functions like data-dependent model selection, data generation and graph visualization; (4) a minor convergence problem of the graphical lasso algorithm is corrected; (5) the package allows the user to apply both lossless and lossy screening rules to scale up large-scale problems, making a tradeoff between computational and statistical efficiency.

Gradient-based Sparse Principal Component Analysis with Extensions to Online Learning

Sparse principal component analysis (PCA) is an important technique for dimensionality reduction of high-dimensional data. However, most existing sparse PCA algorithms are based on non-convex optimization, which provide little guarantee on the global convergence. Sparse PCA algorithms based on a convex formulation, for example the Fantope projection and selection (FPS), overcome this difficulty, but are computationally expensive. In this work we study sparse PCA based on the convex FPS formulation, and propose a new algorithm that is computationally efficient and applicable to large and high-dimensional data sets. Nonasymptotic and explicit bounds are derived for both the optimization error and the statistical accuracy, which can be used for testing and inference problems. We also extend our algorithm to online learning problems, where data are obtained in a streaming fashion. The proposed algorithm is applied to high-dimensional gene expression data for the detection of functional gene groups.

Stability Approach to Regularization Selection (StARS) for High Dimensional Graphical Models

A challenging problem in estimating high-dimensional graphical models is to choose the regularization parameter in a data-dependent way. The standard techniques include $K$-fold cross-validation ($K$-CV), Akaike information criterion (AIC), and Bayesian information criterion (BIC). Though these methods work well for low-dimensional problems, they are not suitable in high dimensional settings. In this paper, we present StARS: a new stability-based method for choosing the regularization parameter in high dimensional inference for undirected graphs. The method has a clear interpretation: we use the least amount of regularization that simultaneously makes a graph sparse and replicable under random sampling. This interpretation requires essentially no conditions. Under mild conditions, we show that StARS is partially sparsistent in terms of graph estimation: i.e. with high probability, all the true edges will be included in the selected model even when the graph size diverges with the sample size. Empirically, the performance of StARS is compared with the state-of-the-art model selection procedures, including $K$-CV, AIC, and BIC, on both synthetic data and a real microarray dataset. StARS outperforms all these competing procedures.

High-dimensional variable selection

This paper explores the following question: what kind of statistical guarantees can be given when doing variable selection in high-dimensional models? In particular, we look at the error rates and power of some multi-stage regression methods. In the first stage we fit a set of candidate models. In the second stage we select one model by cross-validation. In the third stage we use hypothesis testing to eliminate some variables. We refer to the first two stages as "screening" and the last stage as "cleaning." We consider three screening methods: the lasso, marginal regression, and forward stepwise regression. Our method gives consistent variable selection under certain conditions.