Joint Fractional Delay and Doppler Frequency Estimator Under Spectrum Wrapping Phenomenon for LEO-ICAN AFDM Signals

With the rapid development of low earth orbit (LEO) satellites, the design of integrated communication and navigation (ICAN) signals has attracted increasing attention, especially in the field of vehicle-to-everything (V2X). As a new-generation waveform, Affine Frequency Division Multiplexing (AFDM) features high robustness against Doppler effects, a simple modulation structure, and low pilot overhead, making it a promising candidate for high-dynamic LEO satellite scenarios. However, LEO-ICAN AFDM signals face challenges in fractional delay and Doppler frequency estimation. Existing studies that ignore its inherent spectrum wrapping phenomenon may lead to deviations of varying degrees in model construction. This paper conducts an in-depth derivation of AFDM's input-output relationship under fractional cases, reveals the envelope characteristics of its equivalent channel, and proposes a joint estimation algorithm based on peak-to-sidelobe power ratio (PSPR) detection and early-late gate (ELG) to estimate fractional Doppler frequency and delay. Simulations show that the algorithm has low complexity, low guard interval overhead, and high precision compared with traditional methods.

Specific Multi-emitter Identification: Theoretical Limits and Low-complexity Design

Specific emitter identification (SEI) distinguishes emitters by utilizing hardware-induced signal imperfections. However, conventional SEI techniques are primarily designed for single-emitter scenarios. This poses a fundamental limitation in distributed wireless networks, where simultaneous transmissions from multiple emitters result in overlapping signals that conventional single-emitter identification methods cannot effectively handle. To overcome this limitation, we present a specific multi-emitter identification (SMEI) framework via multi-label learning, treating identification as a problem of directly decoding emitter states from overlapping signals. Theoretically, we establish performance bounds using Fano's inequality. Methodologically, the multi-label formulation reduces output dimensionality from exponential to linear scale, thereby substantially decreasing computational complexity. Additionally, we propose an improved SMEI (I-SMEI), which incorporates multi-head attention to effectively capture features in correlated signal combinations. Experimental results demonstrate that SMEI achieves high identification accuracy with a linear computational complexity. Furthermore, the proposed I-SMEI scheme significantly improves identification accuracy across various overlapping scenarios compared to the proposed SMEI and other advanced methods.

Specific multi-emitter identification via multi-label learning

Specific emitter identification leverages hardware-induced impairments to uniquely determine a specific transmitter. However, existing approaches fail to address scenarios where signals from multiple emitters overlap. In this paper, we propose a specific multi-emitter identification (SMEI) method via multi-label learning to determine multiple transmitters. Specifically, the multi-emitter fingerprint extractor is designed to mitigate the mutual interference among overlapping signals. Then, the multi-emitter decision maker is proposed to assign the all emitter identification using the previous extracted fingerprint. Experimental results demonstrate that, compared with baseline approach, the proposed SMEI scheme achieves comparable identification accuracy under various overlapping conditions, while operating at significantly lower complexity. The significance of this paper is to identify multiple emitters from overlapped signal with a low complexity.

StablePCA: Learning Shared Representations across Multiple Sources via Minimax Optimization

When synthesizing multisource high-dimensional data, a key objective is to extract low-dimensional feature representations that effectively approximate the original features across different sources. Such general feature extraction facilitates the discovery of transferable knowledge, mitigates systematic biases such as batch effects, and promotes fairness. In this paper, we propose Stable Principal Component Analysis (StablePCA), a novel method for group distributionally robust learning of latent representations from high-dimensional multi-source data. A primary challenge in generalizing PCA to the multi-source regime lies in the nonconvexity of the fixed rank constraint, rendering the minimax optimization nonconvex. To address this challenge, we employ the Fantope relaxation, reformulating the problem as a convex minimax optimization, with the objective defined as the maximum loss across sources. To solve the relaxed formulation, we devise an optimistic-gradient Mirror Prox algorithm with explicit closed-form updates. Theoretically, we establish the global convergence of the Mirror Prox algorithm, with the convergence rate provided from the optimization perspective. Furthermore, we offer practical criteria to assess how closely the solution approximates the original nonconvex formulation. Through extensive numerical experiments, we demonstrate StablePCA's high accuracy and efficiency in extracting robust low-dimensional representations across various finite-sample scenarios.

Winners with Confidence: Discrete Argmin Inference with an Application to Model Selection

We study the problem of finding the index of the minimum value of a vector from noisy observations. This problem is relevant in population/policy comparison, discrete maximum likelihood, and model selection. We develop a test statistic that is asymptotically normal, even in high-dimensional settings and with potentially many ties in the population mean vector, by integrating concepts and tools from cross-validation and differential privacy. The key technical ingredient is a central limit theorem for globally dependent data. We also propose practical ways to select the tuning parameter that adapts to the signal landscape.

Online Estimation with Rolling Validation: Adaptive Nonparametric Estimation with Stream Data

Online nonparametric estimators are gaining popularity due to their efficient computation and competitive generalization abilities. An important example includes variants of stochastic gradient descent. These algorithms often take one sample point at a time and instantly update the parameter estimate of interest. In this work we consider model selection and hyperparameter tuning for such online algorithms. We propose a weighted rolling-validation procedure, an online variant of leave-one-out cross-validation, that costs minimal extra computation for many typical stochastic gradient descent estimators. Similar to batch cross-validation, it can boost base estimators to achieve a better, adaptive convergence rate. Our theoretical analysis is straightforward, relying mainly on some general statistical stability assumptions. The simulation study underscores the significance of diverging weights in rolling validation in practice and demonstrates its sensitivity even when there is only a slim difference between candidate estimators.

Detecting Errors in Numerical Data via any Regression Model

Noise plagues many numerical datasets, where the recorded values in the data may fail to match the true underlying values due to reasons including: erroneous sensors, data entry/processing mistakes, or imperfect human estimates. Here we consider estimating which data values are incorrect along a numerical column. We present a model-agnostic approach that can utilize any regressor (i.e. statistical or machine learning model) which was fit to predict values in this column based on the other variables in the dataset. By accounting for various uncertainties, our approach distinguishes between genuine anomalies and natural data fluctuations, conditioned on the available information in the dataset. We establish theoretical guarantees for our method and show that other approaches like conformal inference struggle to detect errors. We also contribute a new error detection benchmark involving 5 regression datasets with real-world numerical errors (for which the true values are also known). In this benchmark and additional simulation studies, our method identifies incorrect values with better precision/recall than other approaches.

A Novel K-Repetition Design for SCMA

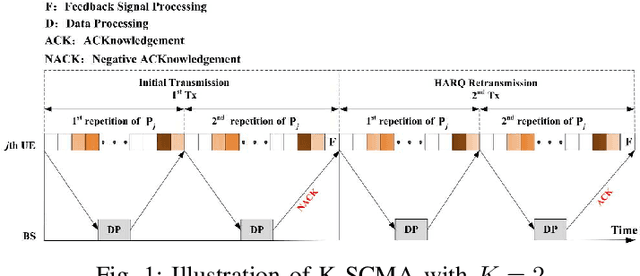
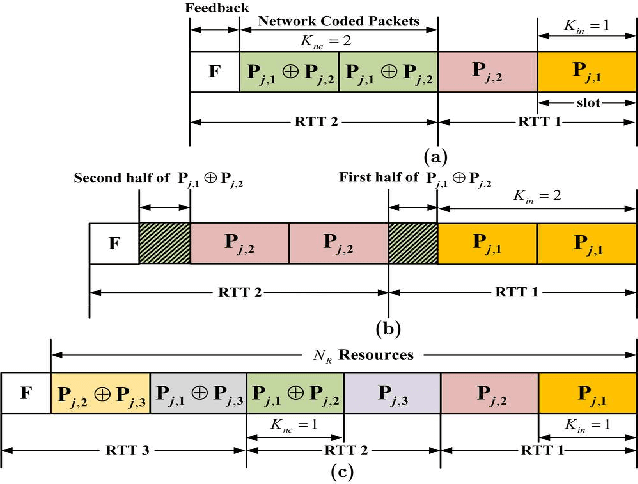
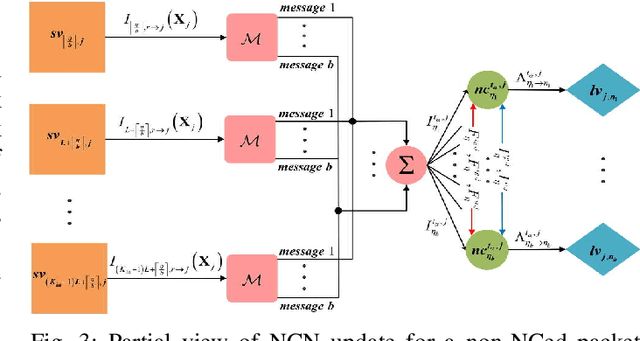
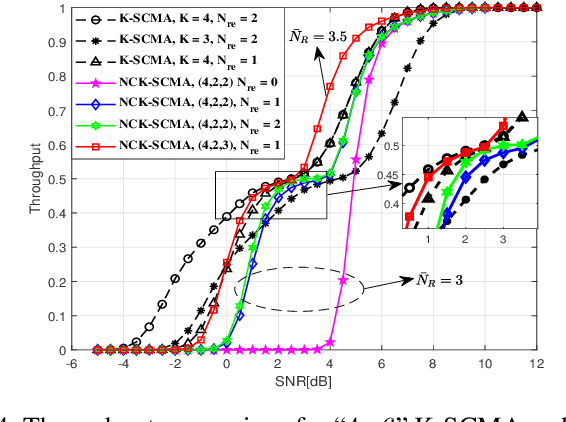
This work presents a novel K-Repetition based HARQ scheme for LDPC coded uplink SCMA by employing a network coding (NC) principle to encode different packets, where K-Repetition is an emerging technique (recommended in 3GPP Release 15) for enhanced reliability and reduced latency in future massive machine-type communication. Such a scheme is referred to as the NC aided K-repetition SCMA (NCK-SCMA). We introduce a joint iterative detection algorithm for improved detection of the data from the proposed LDPC coded NCKSCMA systems. Simulation results demonstrate the benefits of NCK-SCMA with higher throughput and improved reliability over the conventional K-Repetition SCMA.

Analyzing Uplink Grant-free Sparse Code Multiple Access System in Massive IoT Networks

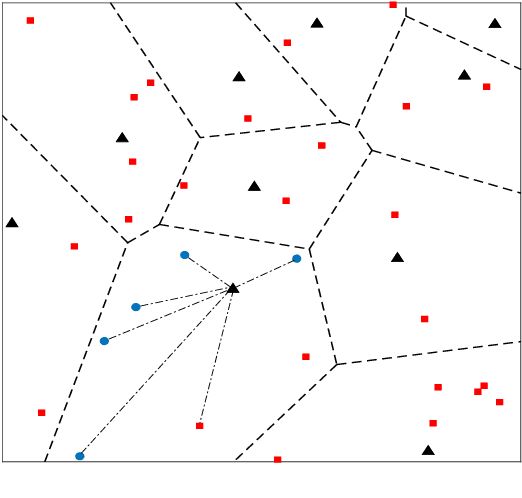
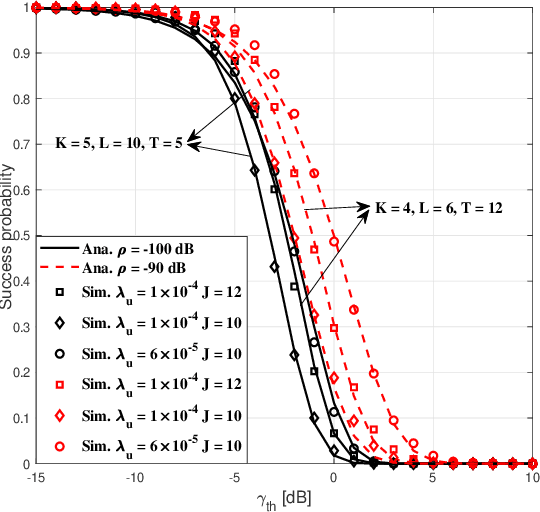
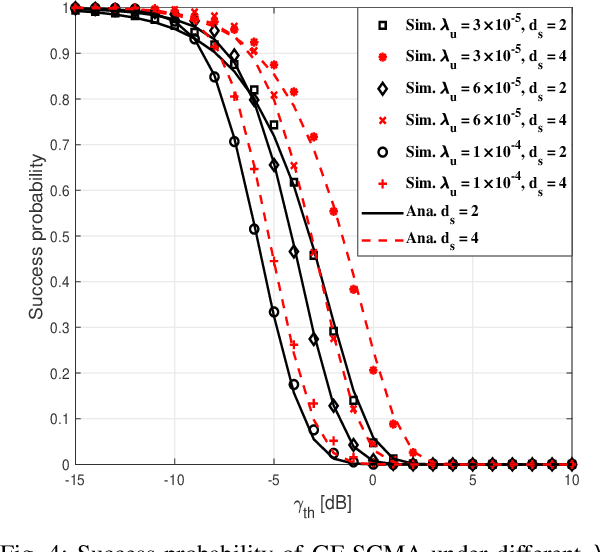
Grant-free sparse code multiple access (GF-SCMA) is considered to be a promising multiple access candidate for future wireless networks. In this paper, we focus on characterizing the performance of uplink GF-SCMA schemes in a network with ubiquitous connections, such as the Internet of Things (IoT) networks. To provide a tractable approach to evaluate the performance of GF-SCMA, we first develop a theoretical model taking into account the property of multi-user detection (MUD) in the SCMA system. We then analyze the error rate performance of GF-SCMA in the case of codebook collision to investigate the reliability of GF-SCMA when reusing codebook in massive IoT networks. For performance evaluation, accurate approximations for both success probability and average symbol error probability (ASEP) are derived. To elaborate further, we utilize the analytical results to discuss the impact of codeword sparse degree in GFSCMA. After that, we conduct a comparative study between SCMA and its variant, dense code multiple access (DCMA), with GF transmission to offer insights into the effectiveness of these two schemes. This facilitates the GF-SCMA system design in practical implementation. Simulation results show that denser codebooks can help to support more UEs and increase the reliability of data transmission in a GF-SCMA network. Moreover, a higher success probability can be achieved by GFSCMA with denser UE deployment at low detection thresholds since SCMA can achieve overloading gain.

Gradient-based Sparse Principal Component Analysis with Extensions to Online Learning

Sparse principal component analysis (PCA) is an important technique for dimensionality reduction of high-dimensional data. However, most existing sparse PCA algorithms are based on non-convex optimization, which provide little guarantee on the global convergence. Sparse PCA algorithms based on a convex formulation, for example the Fantope projection and selection (FPS), overcome this difficulty, but are computationally expensive. In this work we study sparse PCA based on the convex FPS formulation, and propose a new algorithm that is computationally efficient and applicable to large and high-dimensional data sets. Nonasymptotic and explicit bounds are derived for both the optimization error and the statistical accuracy, which can be used for testing and inference problems. We also extend our algorithm to online learning problems, where data are obtained in a streaming fashion. The proposed algorithm is applied to high-dimensional gene expression data for the detection of functional gene groups.