Adaptive Learning of the Latent Space of Wasserstein Generative Adversarial Networks

Generative models based on latent variables, such as generative adversarial networks (GANs) and variational auto-encoders (VAEs), have gained lots of interests due to their impressive performance in many fields. However, many data such as natural images usually do not populate the ambient Euclidean space but instead reside in a lower-dimensional manifold. Thus an inappropriate choice of the latent dimension fails to uncover the structure of the data, possibly resulting in mismatch of latent representations and poor generative qualities. Towards addressing these problems, we propose a novel framework called the latent Wasserstein GAN (LWGAN) that fuses the Wasserstein auto-encoder and the Wasserstein GAN so that the intrinsic dimension of the data manifold can be adaptively learned by a modified informative latent distribution. We prove that there exist an encoder network and a generator network in such a way that the intrinsic dimension of the learned encoding distribution is equal to the dimension of the data manifold. We theoretically establish that our estimated intrinsic dimension is a consistent estimate of the true dimension of the data manifold. Meanwhile, we provide an upper bound on the generalization error of LWGAN, implying that we force the synthetic data distribution to be similar to the real data distribution from a population perspective. Comprehensive empirical experiments verify our framework and show that LWGAN is able to identify the correct intrinsic dimension under several scenarios, and simultaneously generate high-quality synthetic data by sampling from the learned latent distribution.

BloomGML: Graph Machine Learning through the Lens of Bilevel Optimization

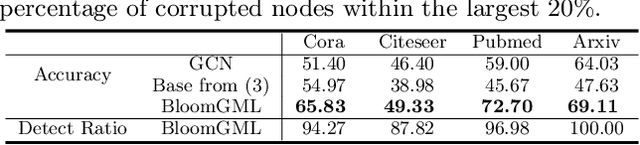
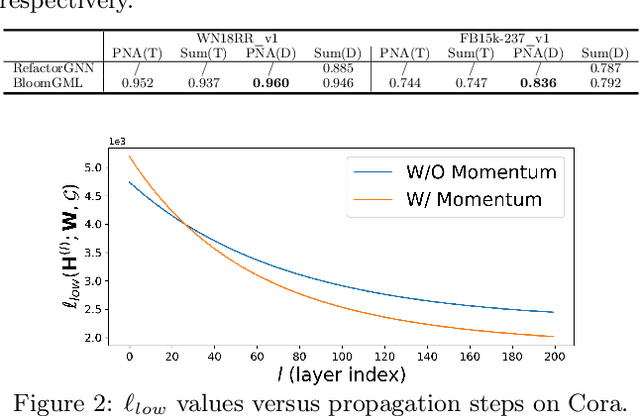
Bilevel optimization refers to scenarios whereby the optimal solution of a lower-level energy function serves as input features to an upper-level objective of interest. These optimal features typically depend on tunable parameters of the lower-level energy in such a way that the entire bilevel pipeline can be trained end-to-end. Although not generally presented as such, this paper demonstrates how a variety of graph learning techniques can be recast as special cases of bilevel optimization or simplifications thereof. In brief, building on prior work we first derive a more flexible class of energy functions that, when paired with various descent steps (e.g., gradient descent, proximal methods, momentum, etc.), form graph neural network (GNN) message-passing layers; critically, we also carefully unpack where any residual approximation error lies with respect to the underlying constituent message-passing functions. We then probe several simplifications of this framework to derive close connections with non-GNN-based graph learning approaches, including knowledge graph embeddings, various forms of label propagation, and efficient graph-regularized MLP models. And finally, we present supporting empirical results that demonstrate the versatility of the proposed bilevel lens, which we refer to as BloomGML, referencing that BiLevel Optimization Offers More Graph Machine Learning. Our code is available at https://github.com/amberyzheng/BloomGML. Let graph ML bloom.

Efficient Multimodal Sampling via Tempered Distribution Flow

Sampling from high-dimensional distributions is a fundamental problem in statistical research and practice. However, great challenges emerge when the target density function is unnormalized and contains isolated modes. We tackle this difficulty by fitting an invertible transformation mapping, called a transport map, between a reference probability measure and the target distribution, so that sampling from the target distribution can be achieved by pushing forward a reference sample through the transport map. We theoretically analyze the limitations of existing transport-based sampling methods using the Wasserstein gradient flow theory, and propose a new method called TemperFlow that addresses the multimodality issue. TemperFlow adaptively learns a sequence of tempered distributions to progressively approach the target distribution, and we prove that it overcomes the limitations of existing methods. Various experiments demonstrate the superior performance of this novel sampler compared to traditional methods, and we show its applications in modern deep learning tasks such as image generation. The programming code for the numerical experiments is available at https://github.com/yixuan/temperflow.

Learning Manifold Dimensions with Conditional Variational Autoencoders

Although the variational autoencoder (VAE) and its conditional extension (CVAE) are capable of state-of-the-art results across multiple domains, their precise behavior is still not fully understood, particularly in the context of data (like images) that lie on or near a low-dimensional manifold. For example, while prior work has suggested that the globally optimal VAE solution can learn the correct manifold dimension, a necessary (but not sufficient) condition for producing samples from the true data distribution, this has never been rigorously proven. Moreover, it remains unclear how such considerations would change when various types of conditioning variables are introduced, or when the data support is extended to a union of manifolds (e.g., as is likely the case for MNIST digits and related). In this work, we address these points by first proving that VAE global minima are indeed capable of recovering the correct manifold dimension. We then extend this result to more general CVAEs, demonstrating practical scenarios whereby the conditioning variables allow the model to adaptively learn manifolds of varying dimension across samples. Our analyses, which have practical implications for various CVAE design choices, are also supported by numerical results on both synthetic and real-world datasets.

Learning Multitask Gaussian Bayesian Networks

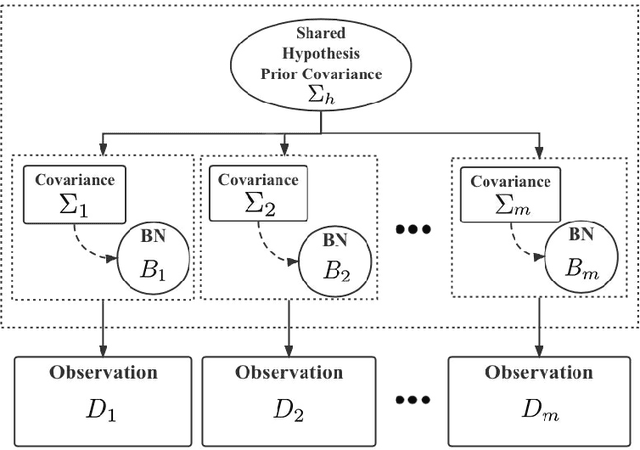
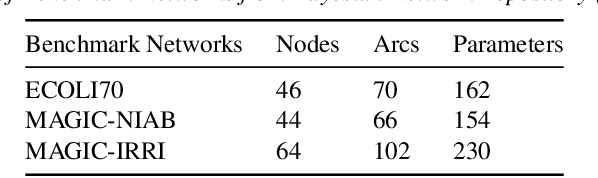
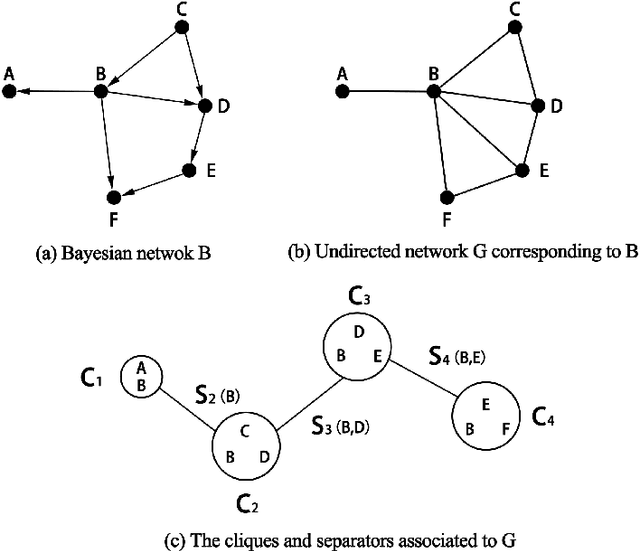
Major depressive disorder (MDD) requires study of brain functional connectivity alterations for patients, which can be uncovered by resting-state functional magnetic resonance imaging (rs-fMRI) data. We consider the problem of identifying alterations of brain functional connectivity for a single MDD patient. This is particularly difficult since the amount of data collected during an fMRI scan is too limited to provide sufficient information for individual analysis. Additionally, rs-fMRI data usually has the characteristics of incompleteness, sparsity, variability, high dimensionality and high noise. To address these problems, we proposed a multitask Gaussian Bayesian network (MTGBN) framework capable for identifying individual disease-induced alterations for MDD patients. We assume that such disease-induced alterations show some degrees of similarity with the tool to learn such network structures from observations to understanding of how system are structured jointly from related tasks. First, we treat each patient in a class of observation as a task and then learn the Gaussian Bayesian networks (GBNs) of this data class by learning from all tasks that share a default covariance matrix that encodes prior knowledge. This setting can help us to learn more information from limited data. Next, we derive a closed-form formula of the complete likelihood function and use the Monte-Carlo Expectation-Maximization(MCEM) algorithm to search for the approximately best Bayesian network structures efficiently. Finally, we assess the performance of our methods with simulated and real-world rs-fMRI data.

Randomized spectral co-clustering for large-scale directed networks

Directed networks are generally used to represent asymmetric relationships among units. Co-clustering aims to cluster the senders and receivers of directed networks simultaneously. In particular, the well-known spectral clustering algorithm could be modified as the spectral co-clustering to co-cluster directed networks. However, large-scale networks pose computational challenge to it. In this paper, we leverage randomized sketching techniques to accelerate the spectral co-clustering algorithms in order to co-cluster large-scale directed networks more efficiently. Specifically, we derive two series of randomized spectral co-clustering algorithms, one is random-projection-based and the other is random-sampling-based. Theoretically, we analyze the resulting algorithms under two generative models\textendash the \emph{stochastic co-block model} and the \emph{degree corrected stochastic co-block model}. The approximation error rates and misclustering error rates are established, which indicate better bounds than the state-of-the-art results of co-clustering literature. Numerically, we conduct simulations to support our theoretical results and test the efficiency of the algorithms on real networks with up to tens of millions of nodes.

Stochastic Approximate Gradient Descent via the Langevin Algorithm

We introduce a novel and efficient algorithm called the stochastic approximate gradient descent (SAGD), as an alternative to the stochastic gradient descent for cases where unbiased stochastic gradients cannot be trivially obtained. Traditional methods for such problems rely on general-purpose sampling techniques such as Markov chain Monte Carlo, which typically requires manual intervention for tuning parameters and does not work efficiently in practice. Instead, SAGD makes use of the Langevin algorithm to construct stochastic gradients that are biased in finite steps but accurate asymptotically, enabling us to theoretically establish the convergence guarantee for SAGD. Inspired by our theoretical analysis, we also provide useful guidelines for its practical implementation. Finally, we show that SAGD performs well experimentally in popular statistical and machine learning problems such as the expectation-maximization algorithm and the variational autoencoders.

Gradient-based Sparse Principal Component Analysis with Extensions to Online Learning

Sparse principal component analysis (PCA) is an important technique for dimensionality reduction of high-dimensional data. However, most existing sparse PCA algorithms are based on non-convex optimization, which provide little guarantee on the global convergence. Sparse PCA algorithms based on a convex formulation, for example the Fantope projection and selection (FPS), overcome this difficulty, but are computationally expensive. In this work we study sparse PCA based on the convex FPS formulation, and propose a new algorithm that is computationally efficient and applicable to large and high-dimensional data sets. Nonasymptotic and explicit bounds are derived for both the optimization error and the statistical accuracy, which can be used for testing and inference problems. We also extend our algorithm to online learning problems, where data are obtained in a streaming fashion. The proposed algorithm is applied to high-dimensional gene expression data for the detection of functional gene groups.