BloomGML: Graph Machine Learning through the Lens of Bilevel Optimization
Paper and Code
Mar 07, 2024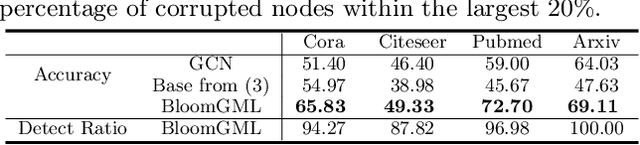


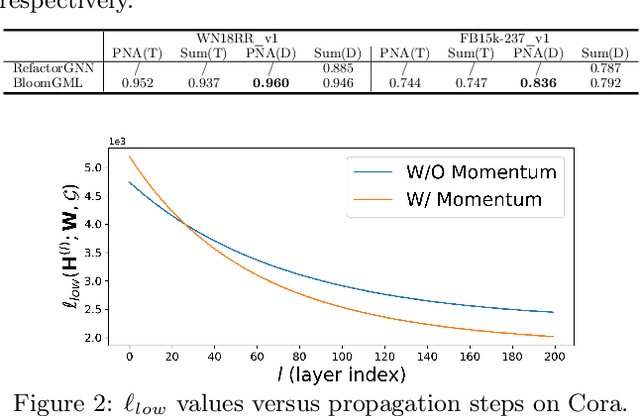
Bilevel optimization refers to scenarios whereby the optimal solution of a lower-level energy function serves as input features to an upper-level objective of interest. These optimal features typically depend on tunable parameters of the lower-level energy in such a way that the entire bilevel pipeline can be trained end-to-end. Although not generally presented as such, this paper demonstrates how a variety of graph learning techniques can be recast as special cases of bilevel optimization or simplifications thereof. In brief, building on prior work we first derive a more flexible class of energy functions that, when paired with various descent steps (e.g., gradient descent, proximal methods, momentum, etc.), form graph neural network (GNN) message-passing layers; critically, we also carefully unpack where any residual approximation error lies with respect to the underlying constituent message-passing functions. We then probe several simplifications of this framework to derive close connections with non-GNN-based graph learning approaches, including knowledge graph embeddings, various forms of label propagation, and efficient graph-regularized MLP models. And finally, we present supporting empirical results that demonstrate the versatility of the proposed bilevel lens, which we refer to as BloomGML, referencing that BiLevel Optimization Offers More Graph Machine Learning. Our code is available at https://github.com/amberyzheng/BloomGML. Let graph ML bloom.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge