Assumption-Lean Post-Integrated Inference with Negative Control Outcomes

Data integration has become increasingly common in aligning multiple heterogeneous datasets. With high-dimensional outcomes, data integration methods aim to extract low-dimensional embeddings of observations to remove unwanted variations, such as batch effects and unmeasured covariates, inherent in data collected from different sources. However, multiple hypothesis testing after data integration can be substantially biased due to the data-dependent integration processes. To address this challenge, we introduce a robust post-integrated inference (PII) method that adjusts for latent heterogeneity using negative control outcomes. By leveraging causal interpretations, we derive nonparametric identification conditions that form the basis of our PII approach. Our assumption-lean semiparametric inference method extends robustness and generality to projected direct effect estimands that account for mediators, confounders, and moderators. These estimands remain statistically meaningful under model misspecifications and with error-prone embeddings. We provide deterministic quantifications of the bias of target estimands induced by estimated embeddings and finite-sample linear expansions of the estimators with uniform concentration bounds on the residuals for all outcomes. The proposed doubly robust estimators are consistent and efficient under minimal assumptions, facilitating data-adaptive estimation with machine learning algorithms. Using random forests, we evaluate empirical statistical errors in simulations and analyze single-cell CRISPR perturbed datasets with potential unmeasured confounders.

Revisiting Optimism and Model Complexity in the Wake of Overparameterized Machine Learning

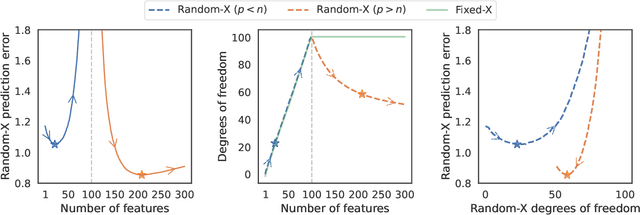
Common practice in modern machine learning involves fitting a large number of parameters relative to the number of observations. These overparameterized models can exhibit surprising generalization behavior, e.g., ``double descent'' in the prediction error curve when plotted against the raw number of model parameters, or another simplistic notion of complexity. In this paper, we revisit model complexity from first principles, by first reinterpreting and then extending the classical statistical concept of (effective) degrees of freedom. Whereas the classical definition is connected to fixed-X prediction error (in which prediction error is defined by averaging over the same, nonrandom covariate points as those used during training), our extension of degrees of freedom is connected to random-X prediction error (in which prediction error is averaged over a new, random sample from the covariate distribution). The random-X setting more naturally embodies modern machine learning problems, where highly complex models, even those complex enough to interpolate the training data, can still lead to desirable generalization performance under appropriate conditions. We demonstrate the utility of our proposed complexity measures through a mix of conceptual arguments, theory, and experiments, and illustrate how they can be used to interpret and compare arbitrary prediction models.

Implicit Regularization Paths of Weighted Neural Representations

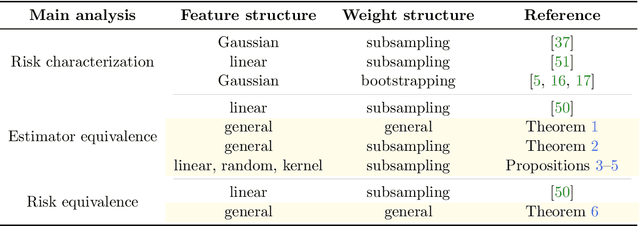
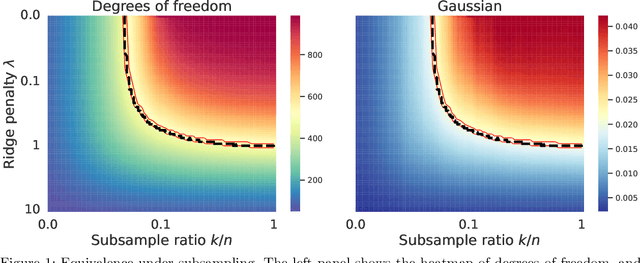
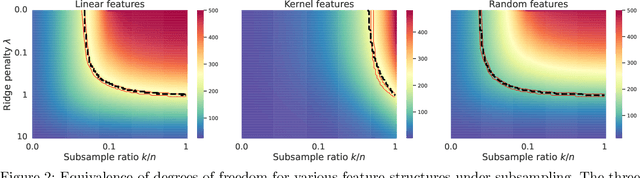
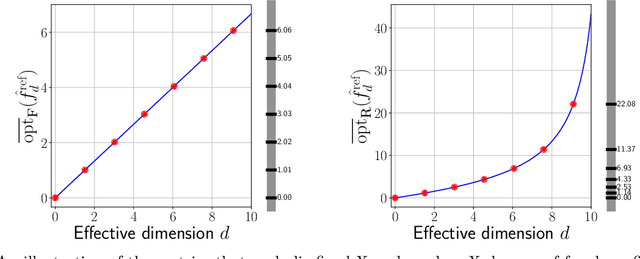
We study the implicit regularization effects induced by (observation) weighting of pretrained features. For weight and feature matrices of bounded operator norms that are infinitesimally free with respect to (normalized) trace functionals, we derive equivalence paths connecting different weighting matrices and ridge regularization levels. Specifically, we show that ridge estimators trained on weighted features along the same path are asymptotically equivalent when evaluated against test vectors of bounded norms. These paths can be interpreted as matching the effective degrees of freedom of ridge estimators fitted with weighted features. For the special case of subsampling without replacement, our results apply to independently sampled random features and kernel features and confirm recent conjectures (Conjectures 7 and 8) of the authors on the existence of such paths in Patil et al. We also present an additive risk decomposition for ensembles of weighted estimators and show that the risks are equivalent along the paths when the ensemble size goes to infinity. As a practical consequence of the path equivalences, we develop an efficient cross-validation method for tuning and apply it to subsampled pretrained representations across several models (e.g., ResNet-50) and datasets (e.g., CIFAR-100).

Distance-Preserving Generative Modeling of Spatial Transcriptomics

Spatial transcriptomics data is invaluable for understanding the spatial organization of gene expression in tissues. There have been consistent efforts in studying how to effectively utilize the associated spatial information for refining gene expression modeling. We introduce a class of distance-preserving generative models for spatial transcriptomics, which utilizes the provided spatial information to regularize the learned representation space of gene expressions to have a similar pair-wise distance structure. This helps the latent space to capture meaningful encodings of genes in spatial proximity. We carry out theoretical analysis over a tractable loss function for this purpose and formalize the overall learning objective as a regularized evidence lower bound. Our framework grants compatibility with any variational-inference-based generative models for gene expression modeling. Empirically, we validate our proposed method on the mouse brain tissues Visium dataset and observe improved performance with variational autoencoders and scVI used as backbone models.

Network-based Neighborhood regression

Given the ubiquity of modularity in biological systems, module-level regulation analysis is vital for understanding biological systems across various levels and their dynamics. Current statistical analysis on biological modules predominantly focuses on either detecting the functional modules in biological networks or sub-group regression on the biological features without using the network data. This paper proposes a novel network-based neighborhood regression framework whose regression functions depend on both the global community-level information and local connectivity structures among entities. An efficient community-wise least square optimization approach is developed to uncover the strength of regulation among the network modules while enabling asymptotic inference. With random graph theory, we derive non-asymptotic estimation error bounds for the proposed estimator, achieving exact minimax optimality. Unlike the root-n consistency typical in canonical linear regression, our model exhibits linear consistency in the number of nodes n, highlighting the advantage of incorporating neighborhood information. The effectiveness of the proposed framework is further supported by extensive numerical experiments. Application to whole-exome sequencing and RNA-sequencing Autism datasets demonstrates the usage of the proposed method in identifying the association between the gene modules of genetic variations and the gene modules of genomic differential expressions.

Causal Inference for Genomic Data with Multiple Heterogeneous Outcomes

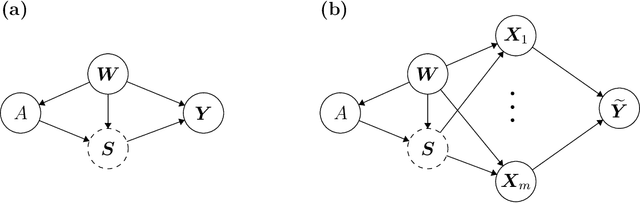
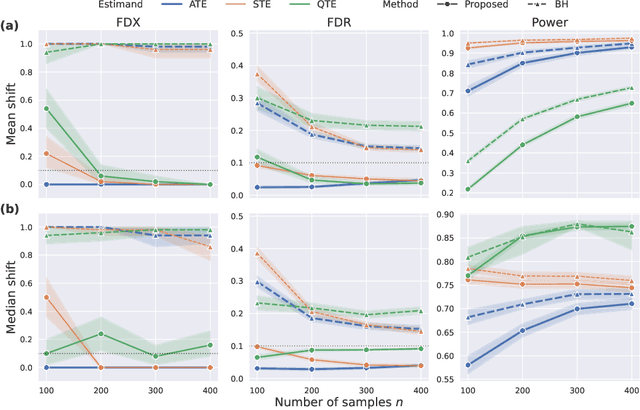
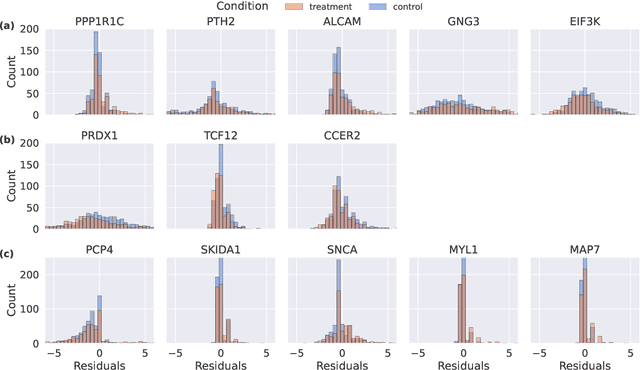
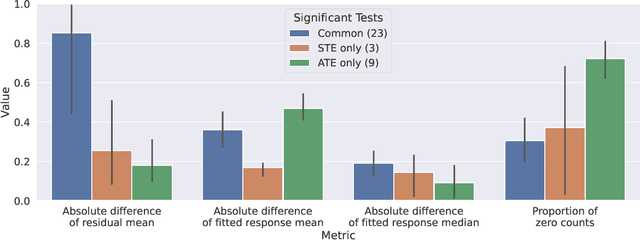
With the evolution of single-cell RNA sequencing techniques into a standard approach in genomics, it has become possible to conduct cohort-level causal inferences based on single-cell-level measurements. However, the individual gene expression levels of interest are not directly observable; instead, only repeated proxy measurements from each individual's cells are available, providing a derived outcome to estimate the underlying outcome for each of many genes. In this paper, we propose a generic semiparametric inference framework for doubly robust estimation with multiple derived outcomes, which also encompasses the usual setting of multiple outcomes when the response of each unit is available. To reliably quantify the causal effects of heterogeneous outcomes, we specialize the analysis to the standardized average treatment effects and the quantile treatment effects. Through this, we demonstrate the use of the semiparametric inferential results for doubly robust estimators derived from both Von Mises expansions and estimating equations. A multiple testing procedure based on the Gaussian multiplier bootstrap is tailored for doubly robust estimators to control the false discovery exceedance rate. Applications in single-cell CRISPR perturbation analysis and individual-level differential expression analysis demonstrate the utility of the proposed methods and offer insights into the usage of different estimands for causal inference in genomics.

Optimal Ridge Regularization for Out-of-Distribution Prediction

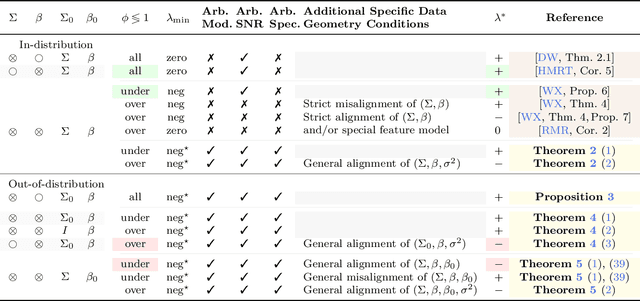
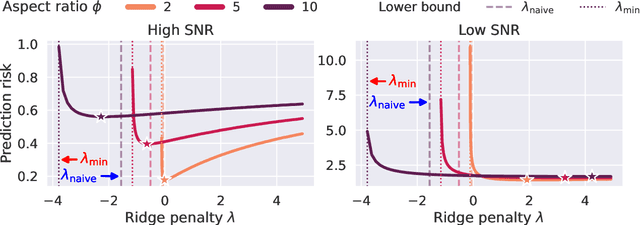
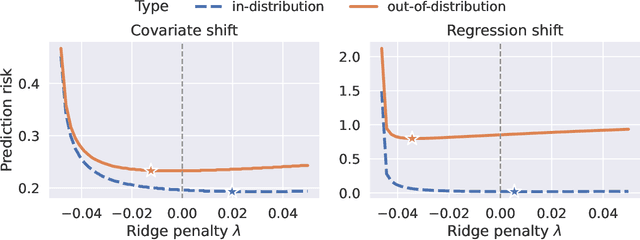
We study the behavior of optimal ridge regularization and optimal ridge risk for out-of-distribution prediction, where the test distribution deviates arbitrarily from the train distribution. We establish general conditions that determine the sign of the optimal regularization level under covariate and regression shifts. These conditions capture the alignment between the covariance and signal structures in the train and test data and reveal stark differences compared to the in-distribution setting. For example, a negative regularization level can be optimal under covariate shift or regression shift, even when the training features are isotropic or the design is underparameterized. Furthermore, we prove that the optimally-tuned risk is monotonic in the data aspect ratio, even in the out-of-distribution setting and when optimizing over negative regularization levels. In general, our results do not make any modeling assumptions for the train or the test distributions, except for moment bounds, and allow for arbitrary shifts and the widest possible range of (negative) regularization levels.

Corrected generalized cross-validation for finite ensembles of penalized estimators

Generalized cross-validation (GCV) is a widely-used method for estimating the squared out-of-sample prediction risk that employs a scalar degrees of freedom adjustment (in a multiplicative sense) to the squared training error. In this paper, we examine the consistency of GCV for estimating the prediction risk of arbitrary ensembles of penalized least squares estimators. We show that GCV is inconsistent for any finite ensemble of size greater than one. Towards repairing this shortcoming, we identify a correction that involves an additional scalar correction (in an additive sense) based on degrees of freedom adjusted training errors from each ensemble component. The proposed estimator (termed CGCV) maintains the computational advantages of GCV and requires neither sample splitting, model refitting, or out-of-bag risk estimation. The estimator stems from a finer inspection of ensemble risk decomposition and two intermediate risk estimators for the components in this decomposition. We provide a non-asymptotic analysis of the CGCV and the two intermediate risk estimators for ensembles of convex penalized estimators under Gaussian features and a linear response model. In the special case of ridge regression, we extend the analysis to general feature and response distributions using random matrix theory, which establishes model-free uniform consistency of CGCV.

Simultaneous inference for generalized linear models with unmeasured confounders

Tens of thousands of simultaneous hypothesis tests are routinely performed in genomic studies to identify differentially expressed genes. However, due to unmeasured confounders, many standard statistical approaches may be substantially biased. This paper investigates the large-scale hypothesis testing problem for multivariate generalized linear models in the presence of confounding effects. Under arbitrary confounding mechanisms, we propose a unified statistical estimation and inference framework that harnesses orthogonal structures and integrates linear projections into three key stages. It begins by disentangling marginal and uncorrelated confounding effects to recover the latent coefficients. Subsequently, latent factors and primary effects are jointly estimated through lasso-type optimization. Finally, we incorporate projected and weighted bias-correction steps for hypothesis testing. Theoretically, we establish the identification conditions of various effects and non-asymptotic error bounds. We show effective Type-I error control of asymptotic $z$-tests as sample and response sizes approach infinity. Numerical experiments demonstrate that the proposed method controls the false discovery rate by the Benjamini-Hochberg procedure and is more powerful than alternative methods. By comparing single-cell RNA-seq counts from two groups of samples, we demonstrate the suitability of adjusting confounding effects when significant covariates are absent from the model.

Generalized equivalences between subsampling and ridge regularization

We establish precise structural and risk equivalences between subsampling and ridge regularization for ensemble ridge estimators. Specifically, we prove that linear and quadratic functionals of subsample ridge estimators, when fitted with different ridge regularization levels $\lambda$ and subsample aspect ratios $\psi$, are asymptotically equivalent along specific paths in the $(\lambda, \psi )$-plane (where $\psi$ is the ratio of the feature dimension to the subsample size). Our results only require bounded moment assumptions on feature and response distributions and allow for arbitrary joint distributions. Furthermore, we provide a datadependent method to determine the equivalent paths of $(\lambda, \psi )$. An indirect implication of our equivalences is that optimally-tuned ridge regression exhibits a monotonic prediction risk in the data aspect ratio. This resolves a recent open problem raised by Nakkiran et al. under general data distributions and a mild regularity condition that maintains regression hardness through linearized signal-to-noise ratios.