GraphCoT-VLA: A 3D Spatial-Aware Reasoning Vision-Language-Action Model for Robotic Manipulation with Ambiguous Instructions

Vision-language-action models have emerged as a crucial paradigm in robotic manipulation. However, existing VLA models exhibit notable limitations in handling ambiguous language instructions and unknown environmental states. Furthermore, their perception is largely constrained to static two-dimensional observations, lacking the capability to model three-dimensional interactions between the robot and its environment. To address these challenges, this paper proposes GraphCoT-VLA, an efficient end-to-end model. To enhance the model's ability to interpret ambiguous instructions and improve task planning, we design a structured Chain-of-Thought reasoning module that integrates high-level task understanding and planning, failed task feedback, and low-level imaginative reasoning about future object positions and robot actions. Additionally, we construct a real-time updatable 3D Pose-Object graph, which captures the spatial configuration of robot joints and the topological relationships between objects in 3D space, enabling the model to better understand and manipulate their interactions. We further integrates a dropout hybrid reasoning strategy to achieve efficient control outputs. Experimental results across multiple real-world robotic tasks demonstrate that GraphCoT-VLA significantly outperforms existing methods in terms of task success rate and response speed, exhibiting strong generalization and robustness in open environments and under uncertain instructions.

Estimating Generalization Performance Along the Trajectory of Proximal SGD in Robust Regression

This paper studies the generalization performance of iterates obtained by Gradient Descent (GD), Stochastic Gradient Descent (SGD) and their proximal variants in high-dimensional robust regression problems. The number of features is comparable to the sample size and errors may be heavy-tailed. We introduce estimators that precisely track the generalization error of the iterates along the trajectory of the iterative algorithm. These estimators are provably consistent under suitable conditions. The results are illustrated through several examples, including Huber regression, pseudo-Huber regression, and their penalized variants with non-smooth regularizer. We provide explicit generalization error estimates for iterates generated from GD and SGD, or from proximal SGD in the presence of a non-smooth regularizer. The proposed risk estimates serve as effective proxies for the actual generalization error, allowing us to determine the optimal stopping iteration that minimizes the generalization error. Extensive simulations confirm the effectiveness of the proposed generalization error estimates.

Uncertainty quantification for iterative algorithms in linear models with application to early stopping

This paper investigates the iterates $\hbb^1,\dots,\hbb^T$ obtained from iterative algorithms in high-dimensional linear regression problems, in the regime where the feature dimension $p$ is comparable with the sample size $n$, i.e., $p \asymp n$. The analysis and proposed estimators are applicable to Gradient Descent (GD), proximal GD and their accelerated variants such as Fast Iterative Soft-Thresholding (FISTA). The paper proposes novel estimators for the generalization error of the iterate $\hbb^t$ for any fixed iteration $t$ along the trajectory. These estimators are proved to be $\sqrt n$-consistent under Gaussian designs. Applications to early-stopping are provided: when the generalization error of the iterates is a U-shape function of the iteration $t$, the estimates allow to select from the data an iteration $\hat t$ that achieves the smallest generalization error along the trajectory. Additionally, we provide a technique for developing debiasing corrections and valid confidence intervals for the components of the true coefficient vector from the iterate $\hbb^t$ at any finite iteration $t$. Extensive simulations on synthetic data illustrate the theoretical results.

A Protein Structure Prediction Approach Leveraging Transformer and CNN Integration

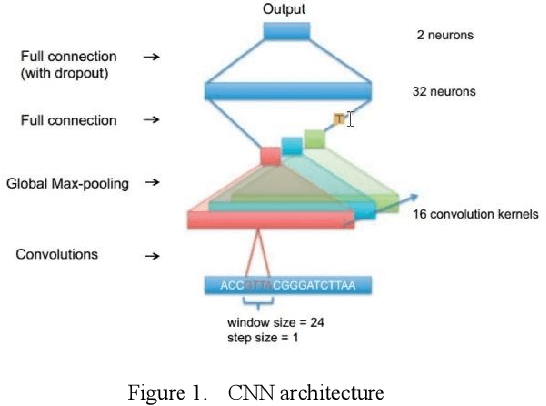
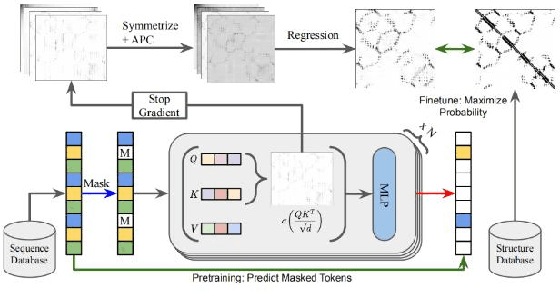
Proteins are essential for life, and their structure determines their function. The protein secondary structure is formed by the folding of the protein primary structure, and the protein tertiary structure is formed by the bending and folding of the secondary structure. Therefore, the study of protein secondary structure is very helpful to the overall understanding of protein structure. Although the accuracy of protein secondary structure prediction has continuously improved with the development of machine learning and deep learning, progress in the field of protein structure prediction, unfortunately, remains insufficient to meet the large demand for protein information. Therefore, based on the advantages of deep learning-based methods in feature extraction and learning ability, this paper adopts a two-dimensional fusion deep neural network model, DstruCCN, which uses Convolutional Neural Networks (CCN) and a supervised Transformer protein language model for single-sequence protein structure prediction. The training features of the two are combined to predict the protein Transformer binding site matrix, and then the three-dimensional structure is reconstructed using energy minimization.

Corrected generalized cross-validation for finite ensembles of penalized estimators

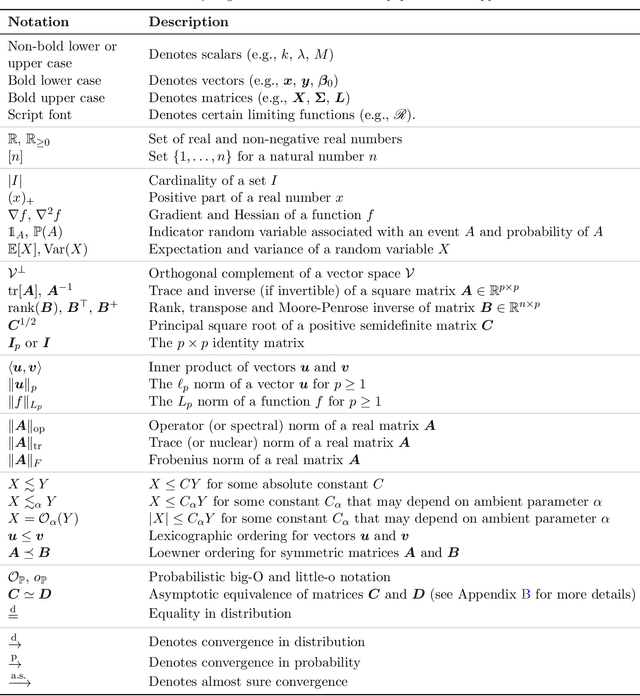
Generalized cross-validation (GCV) is a widely-used method for estimating the squared out-of-sample prediction risk that employs a scalar degrees of freedom adjustment (in a multiplicative sense) to the squared training error. In this paper, we examine the consistency of GCV for estimating the prediction risk of arbitrary ensembles of penalized least squares estimators. We show that GCV is inconsistent for any finite ensemble of size greater than one. Towards repairing this shortcoming, we identify a correction that involves an additional scalar correction (in an additive sense) based on degrees of freedom adjusted training errors from each ensemble component. The proposed estimator (termed CGCV) maintains the computational advantages of GCV and requires neither sample splitting, model refitting, or out-of-bag risk estimation. The estimator stems from a finer inspection of ensemble risk decomposition and two intermediate risk estimators for the components in this decomposition. We provide a non-asymptotic analysis of the CGCV and the two intermediate risk estimators for ensembles of convex penalized estimators under Gaussian features and a linear response model. In the special case of ridge regression, we extend the analysis to general feature and response distributions using random matrix theory, which establishes model-free uniform consistency of CGCV.

Multinomial Logistic Regression: Asymptotic Normality on Null Covariates in High-Dimensions

This paper investigates the asymptotic distribution of the maximum-likelihood estimate (MLE) in multinomial logistic models in the high-dimensional regime where dimension and sample size are of the same order. While classical large-sample theory provides asymptotic normality of the MLE under certain conditions, such classical results are expected to fail in high-dimensions as documented for the binary logistic case in the seminal work of Sur and Cand\`es [2019]. We address this issue in classification problems with 3 or more classes, by developing asymptotic normality and asymptotic chi-square results for the multinomial logistic MLE (also known as cross-entropy minimizer) on null covariates. Our theory leads to a new methodology to test the significance of a given feature. Extensive simulation studies on synthetic data corroborate these asymptotic results and confirm the validity of proposed p-values for testing the significance of a given feature.

Noise Covariance Estimation in Multi-Task High-dimensional Linear Models

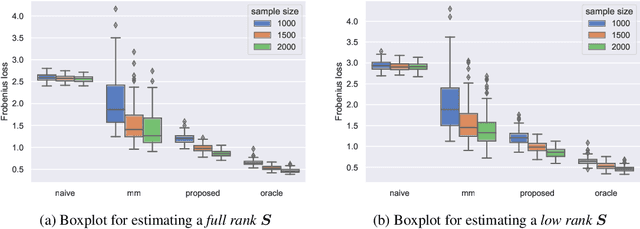
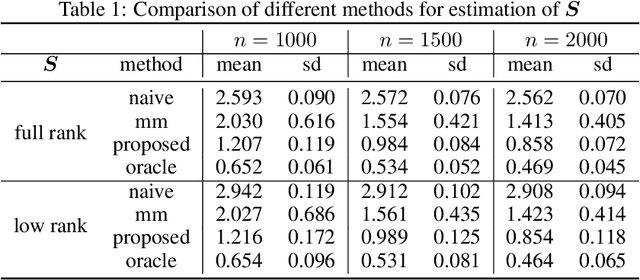
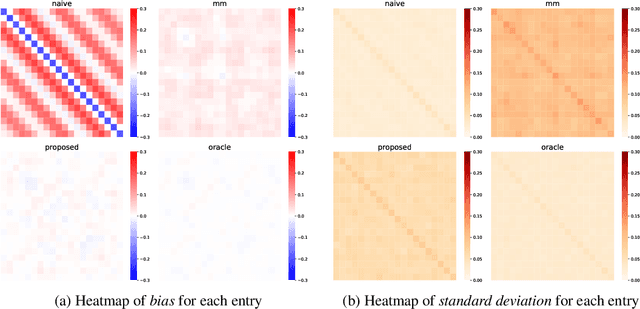
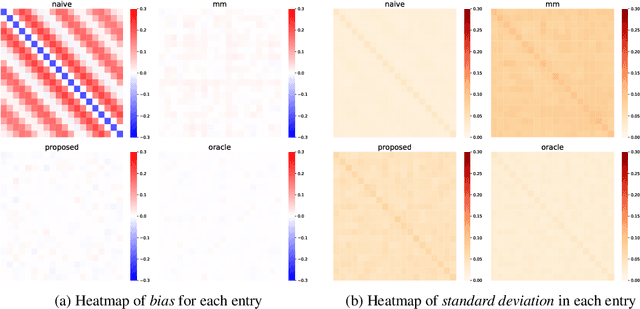
This paper studies the multi-task high-dimensional linear regression models where the noise among different tasks is correlated, in the moderately high dimensional regime where sample size $n$ and dimension $p$ are of the same order. Our goal is to estimate the covariance matrix of the noise random vectors, or equivalently the correlation of the noise variables on any pair of two tasks. Treating the regression coefficients as a nuisance parameter, we leverage the multi-task elastic-net and multi-task lasso estimators to estimate the nuisance. By precisely understanding the bias of the squared residual matrix and by correcting this bias, we develop a novel estimator of the noise covariance that converges in Frobenius norm at the rate $n^{-1/2}$ when the covariates are Gaussian. This novel estimator is efficiently computable. Under suitable conditions, the proposed estimator of the noise covariance attains the same rate of convergence as the "oracle" estimator that knows in advance the regression coefficients of the multi-task model. The Frobenius error bounds obtained in this paper also illustrate the advantage of this new estimator compared to a method-of-moments estimator that does not attempt to estimate the nuisance. As a byproduct of our techniques, we obtain an estimate of the generalization error of the multi-task elastic-net and multi-task lasso estimators. Extensive simulation studies are carried out to illustrate the numerical performance of the proposed method.