Noise Covariance Estimation in Multi-Task High-dimensional Linear Models
Paper and Code
Jun 15, 2022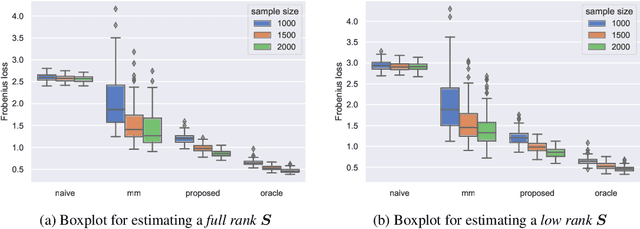
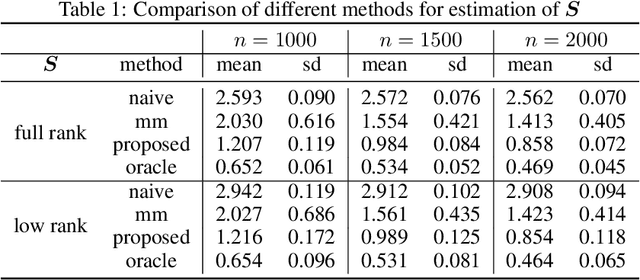
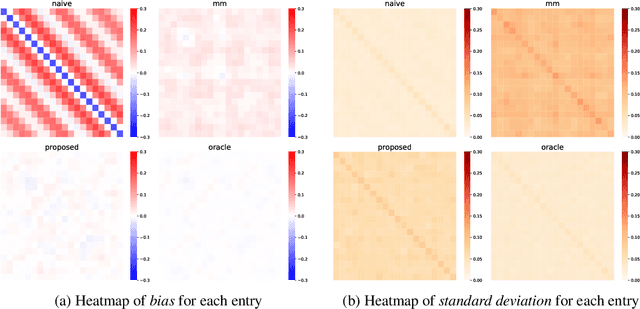
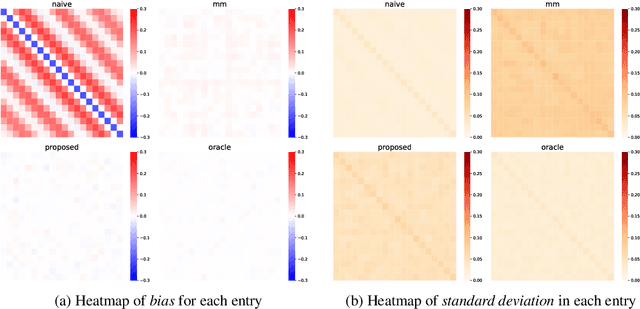
This paper studies the multi-task high-dimensional linear regression models where the noise among different tasks is correlated, in the moderately high dimensional regime where sample size $n$ and dimension $p$ are of the same order. Our goal is to estimate the covariance matrix of the noise random vectors, or equivalently the correlation of the noise variables on any pair of two tasks. Treating the regression coefficients as a nuisance parameter, we leverage the multi-task elastic-net and multi-task lasso estimators to estimate the nuisance. By precisely understanding the bias of the squared residual matrix and by correcting this bias, we develop a novel estimator of the noise covariance that converges in Frobenius norm at the rate $n^{-1/2}$ when the covariates are Gaussian. This novel estimator is efficiently computable. Under suitable conditions, the proposed estimator of the noise covariance attains the same rate of convergence as the "oracle" estimator that knows in advance the regression coefficients of the multi-task model. The Frobenius error bounds obtained in this paper also illustrate the advantage of this new estimator compared to a method-of-moments estimator that does not attempt to estimate the nuisance. As a byproduct of our techniques, we obtain an estimate of the generalization error of the multi-task elastic-net and multi-task lasso estimators. Extensive simulation studies are carried out to illustrate the numerical performance of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge