Noise Covariance Estimation in Multi-Task High-dimensional Linear Models

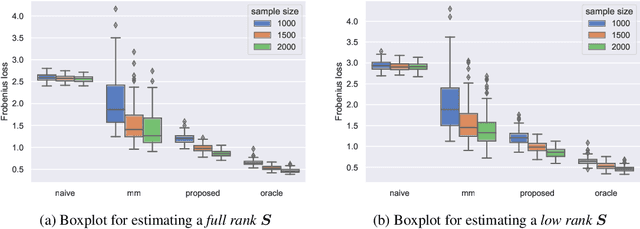
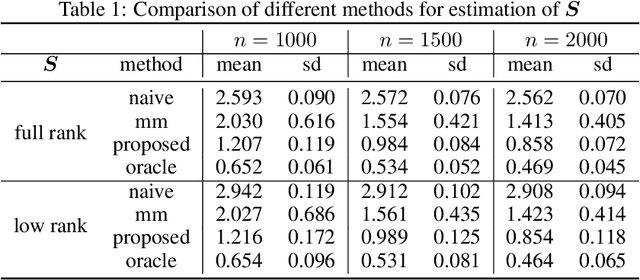
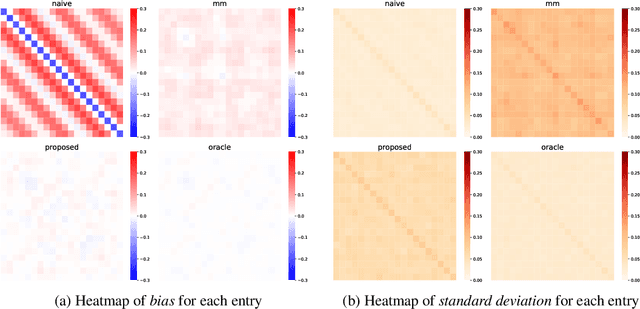
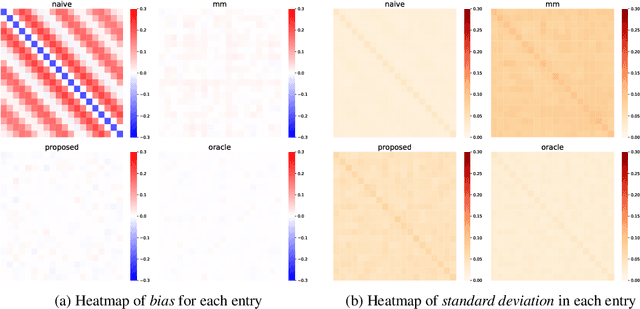
This paper studies the multi-task high-dimensional linear regression models where the noise among different tasks is correlated, in the moderately high dimensional regime where sample size $n$ and dimension $p$ are of the same order. Our goal is to estimate the covariance matrix of the noise random vectors, or equivalently the correlation of the noise variables on any pair of two tasks. Treating the regression coefficients as a nuisance parameter, we leverage the multi-task elastic-net and multi-task lasso estimators to estimate the nuisance. By precisely understanding the bias of the squared residual matrix and by correcting this bias, we develop a novel estimator of the noise covariance that converges in Frobenius norm at the rate $n^{-1/2}$ when the covariates are Gaussian. This novel estimator is efficiently computable. Under suitable conditions, the proposed estimator of the noise covariance attains the same rate of convergence as the "oracle" estimator that knows in advance the regression coefficients of the multi-task model. The Frobenius error bounds obtained in this paper also illustrate the advantage of this new estimator compared to a method-of-moments estimator that does not attempt to estimate the nuisance. As a byproduct of our techniques, we obtain an estimate of the generalization error of the multi-task elastic-net and multi-task lasso estimators. Extensive simulation studies are carried out to illustrate the numerical performance of the proposed method.

Chi-square and normal inference in high-dimensional multi-task regression

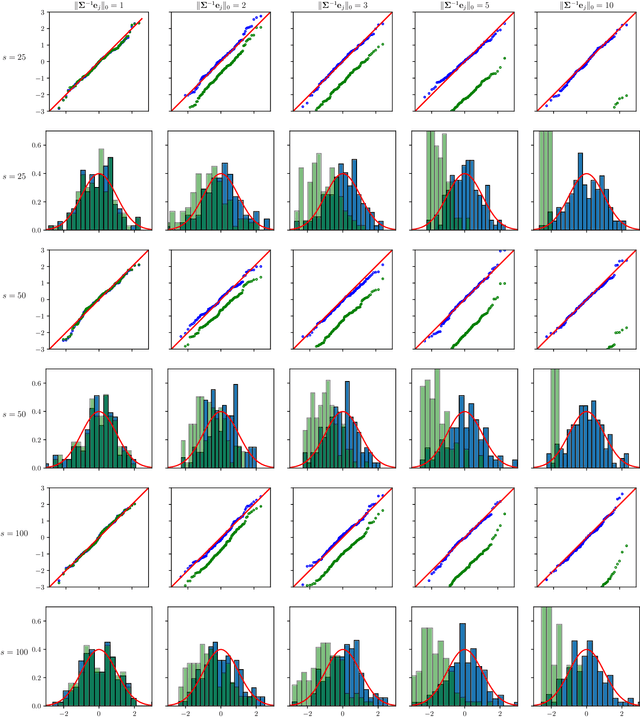
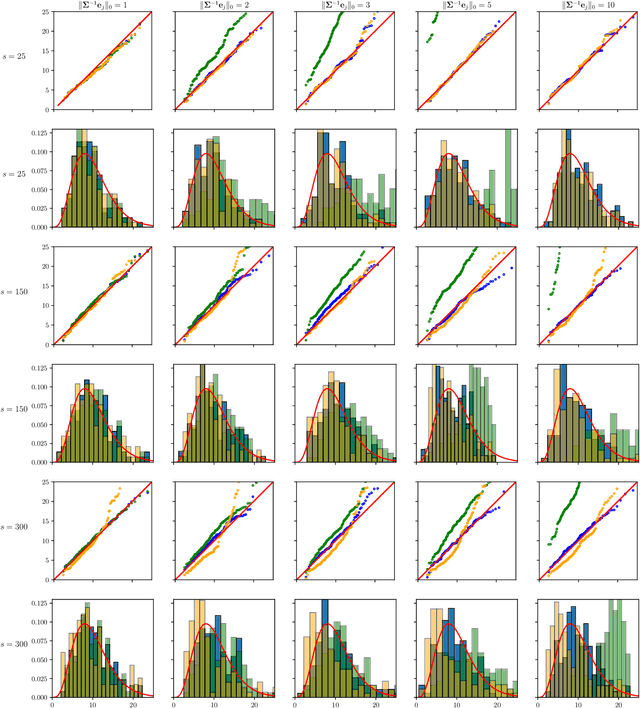
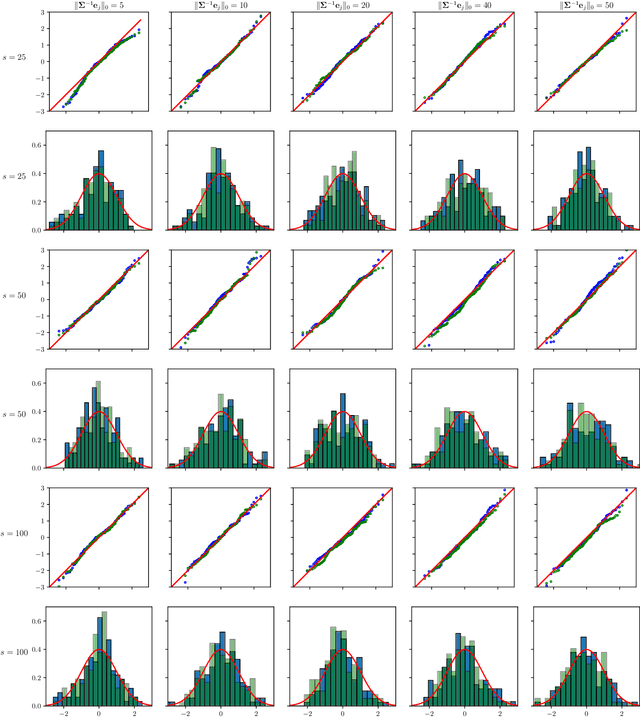
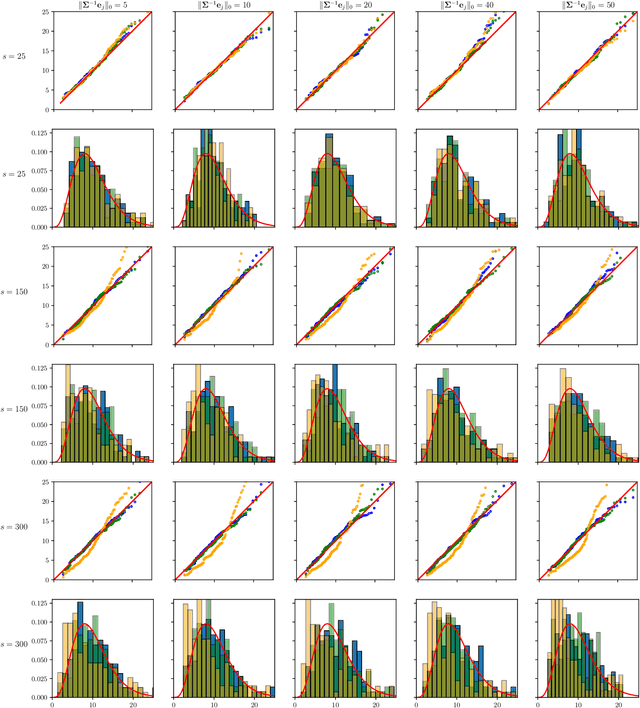
The paper proposes chi-square and normal inference methodologies for the unknown coefficient matrix $B^*$ of size $p\times T$ in a Multi-Task (MT) linear model with $p$ covariates, $T$ tasks and $n$ observations under a row-sparse assumption on $B^*$. The row-sparsity $s$, dimension $p$ and number of tasks $T$ are allowed to grow with $n$. In the high-dimensional regime $p\ggg n$, in order to leverage row-sparsity, the MT Lasso is considered. We build upon the MT Lasso with a de-biasing scheme to correct for the bias induced by the penalty. This scheme requires the introduction of a new data-driven object, coined the interaction matrix, that captures effective correlations between noise vector and residuals on different tasks. This matrix is psd, of size $T\times T$ and can be computed efficiently. The interaction matrix lets us derive asymptotic normal and $\chi^2_T$ results under Gaussian design and $\frac{sT+s\log(p/s)}{n}\to0$ which corresponds to consistency in Frobenius norm. These asymptotic distribution results yield valid confidence intervals for single entries of $B^*$ and valid confidence ellipsoids for single rows of $B^*$, for both known and unknown design covariance $\Sigma$. While previous proposals in grouped-variables regression require row-sparsity $s\lesssim\sqrt n$ up to constants depending on $T$ and logarithmic factors in $n,p$, the de-biasing scheme using the interaction matrix provides confidence intervals and $\chi^2_T$ confidence ellipsoids under the conditions ${\min(T^2,\log^8p)}/{n}\to 0$ and $$ \frac{sT+s\log(p/s)+\|\Sigma^{-1}e_j\|_0\log p}{n}\to0, \quad \frac{\min(s,\|\Sigma^{-1}e_j\|_0)}{\sqrt n} \sqrt{[T+\log(p/s)]\log p}\to 0, $$ allowing row-sparsity $s\ggg\sqrt n$ when $\|\Sigma^{-1}e_j\|_0 \sqrt T\lll \sqrt{n}$ up to logarithmic factors.