Chi-square and normal inference in high-dimensional multi-task regression
Paper and Code
Jul 16, 2021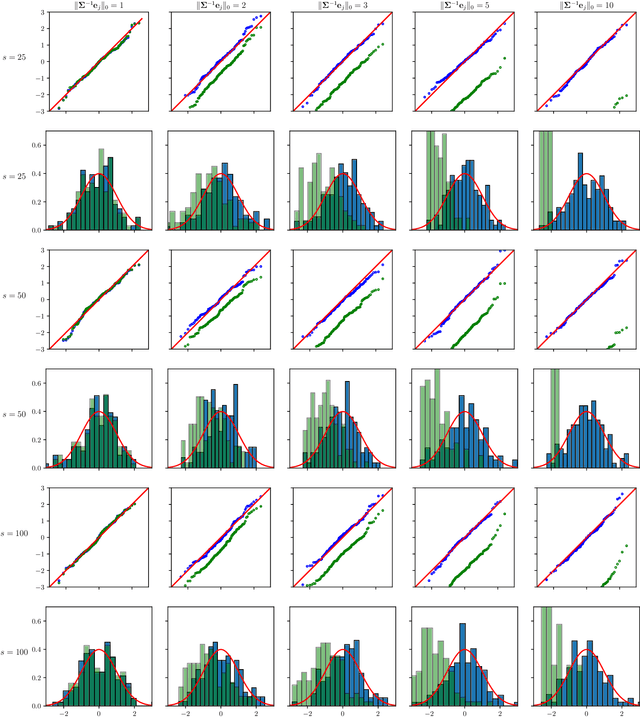
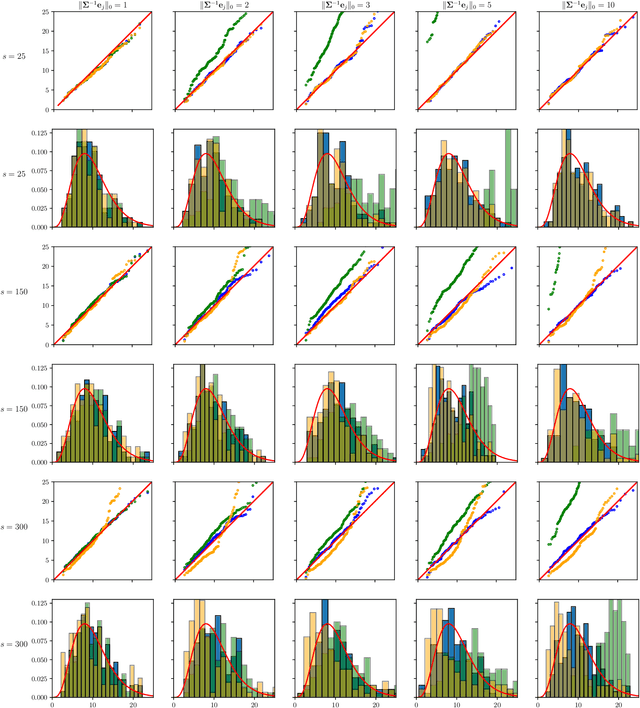
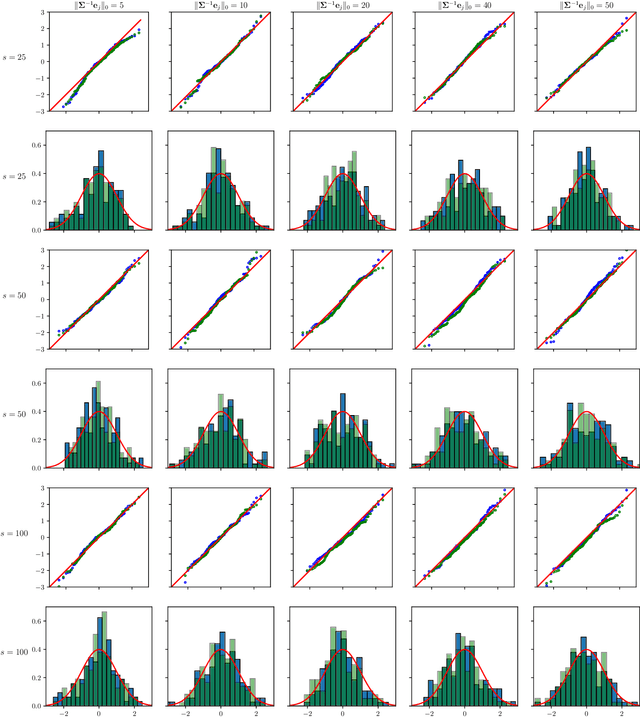
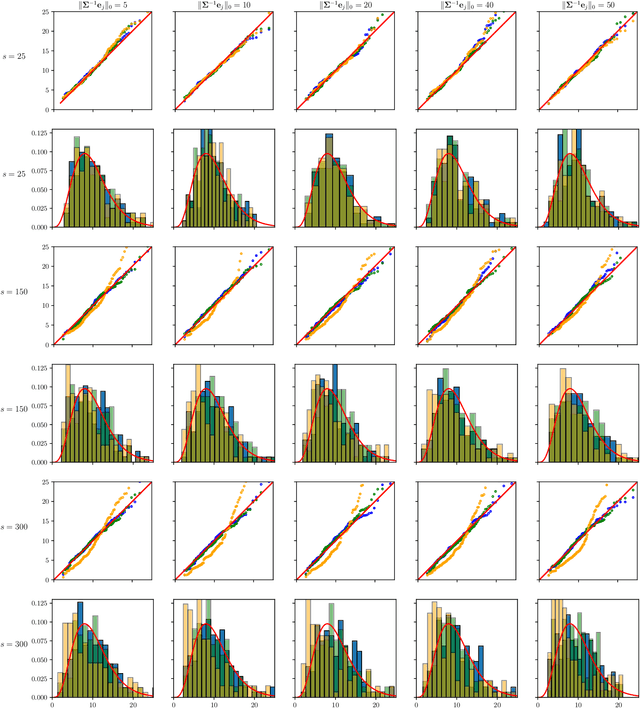
The paper proposes chi-square and normal inference methodologies for the unknown coefficient matrix $B^*$ of size $p\times T$ in a Multi-Task (MT) linear model with $p$ covariates, $T$ tasks and $n$ observations under a row-sparse assumption on $B^*$. The row-sparsity $s$, dimension $p$ and number of tasks $T$ are allowed to grow with $n$. In the high-dimensional regime $p\ggg n$, in order to leverage row-sparsity, the MT Lasso is considered. We build upon the MT Lasso with a de-biasing scheme to correct for the bias induced by the penalty. This scheme requires the introduction of a new data-driven object, coined the interaction matrix, that captures effective correlations between noise vector and residuals on different tasks. This matrix is psd, of size $T\times T$ and can be computed efficiently. The interaction matrix lets us derive asymptotic normal and $\chi^2_T$ results under Gaussian design and $\frac{sT+s\log(p/s)}{n}\to0$ which corresponds to consistency in Frobenius norm. These asymptotic distribution results yield valid confidence intervals for single entries of $B^*$ and valid confidence ellipsoids for single rows of $B^*$, for both known and unknown design covariance $\Sigma$. While previous proposals in grouped-variables regression require row-sparsity $s\lesssim\sqrt n$ up to constants depending on $T$ and logarithmic factors in $n,p$, the de-biasing scheme using the interaction matrix provides confidence intervals and $\chi^2_T$ confidence ellipsoids under the conditions ${\min(T^2,\log^8p)}/{n}\to 0$ and $$ \frac{sT+s\log(p/s)+\|\Sigma^{-1}e_j\|_0\log p}{n}\to0, \quad \frac{\min(s,\|\Sigma^{-1}e_j\|_0)}{\sqrt n} \sqrt{[T+\log(p/s)]\log p}\to 0, $$ allowing row-sparsity $s\ggg\sqrt n$ when $\|\Sigma^{-1}e_j\|_0 \sqrt T\lll \sqrt{n}$ up to logarithmic factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge