Robust semi-parametric signal detection in particle physics with classifiers decorrelated via optimal transport

Searches of new signals in particle physics are usually done by training a supervised classifier to separate a signal model from the known Standard Model physics (also called the background model). However, even when the signal model is correct, systematic errors in the background model can influence supervised classifiers and might adversely affect the signal detection procedure. To tackle this problem, one approach is to use the (possibly misspecified) classifier only to perform a preliminary signal-enrichment step and then to carry out a bump hunt on the signal-rich sample using only the real experimental data. For this procedure to work, we need a classifier constrained to be decorrelated with one or more protected variables used for the signal detection step. We do this by considering an optimal transport map of the classifier output that makes it independent of the protected variable(s) for the background. We then fit a semi-parametric mixture model to the distribution of the protected variable after making cuts on the transformed classifier to detect the presence of a signal. We compare and contrast this decorrelation method with previous approaches, show that the decorrelation procedure is robust to moderate background misspecification, and analyse the power of the signal detection test as a function of the cut on the classifier.

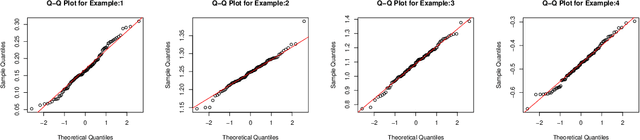
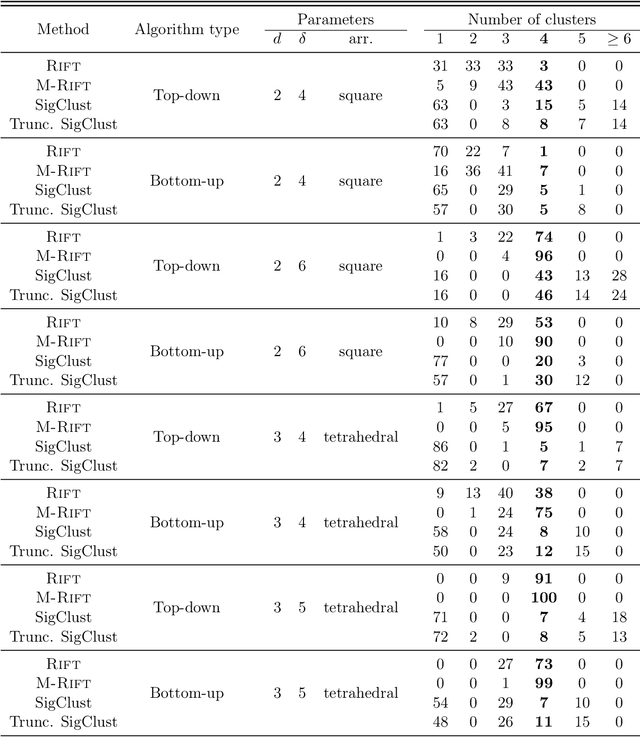
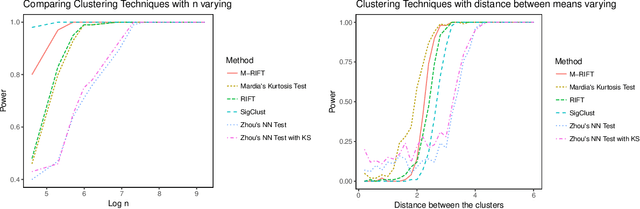
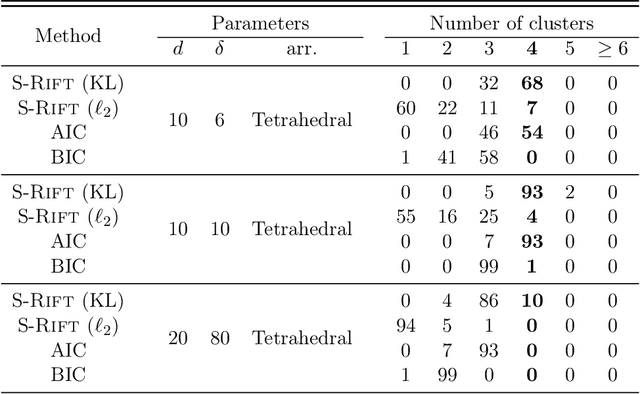
Gaussian Mixture Clustering Using Relative Tests of Fit

We consider clustering based on significance tests for Gaussian Mixture Models (GMMs). Our starting point is the SigClust method developed by Liu et al. (2008), which introduces a test based on the k-means objective (with k = 2) to decide whether the data should be split into two clusters. When applied recursively, this test yields a method for hierarchical clustering that is equipped with a significance guarantee. We study the limiting distribution and power of this approach in some examples and show that there are large regions of the parameter space where the power is low. We then introduce a new test based on the idea of relative fit. Unlike prior work, we test for whether a mixture of Gaussians provides a better fit relative to a single Gaussian, without assuming that either model is correct. The proposed test has a simple critical value and provides provable error control. One version of our test provides exact, finite sample control of the type I error. We show how our tests can be used for hierarchical clustering as well as in a sequential manner for model selection. We conclude with an extensive simulation study and a cluster analysis of a gene expression dataset.

A Generalization of Convolutional Neural Networks to Graph-Structured Data

This paper introduces a generalization of Convolutional Neural Networks (CNNs) from low-dimensional grid data, such as images, to graph-structured data. We propose a novel spatial convolution utilizing a random walk to uncover the relations within the input, analogous to the way the standard convolution uses the spatial neighborhood of a pixel on the grid. The convolution has an intuitive interpretation, is efficient and scalable and can also be used on data with varying graph structure. Furthermore, this generalization can be applied to many standard regression or classification problems, by learning the the underlying graph. We empirically demonstrate the performance of the proposed CNN on MNIST, and challenge the state-of-the-art on Merck molecular activity data set.