Confidence Intervals for Selected Parameters

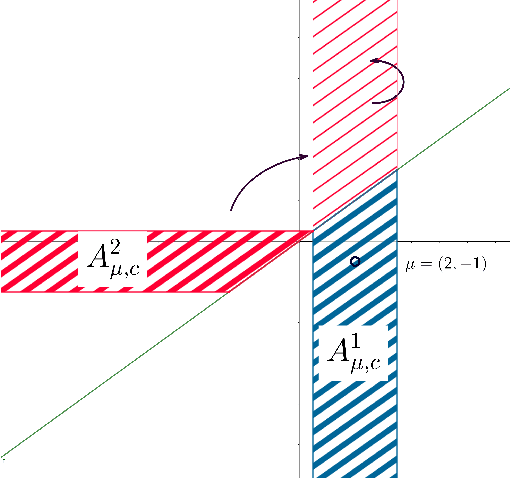
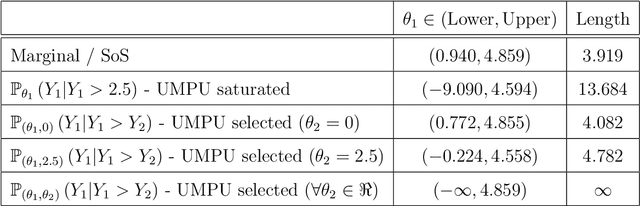
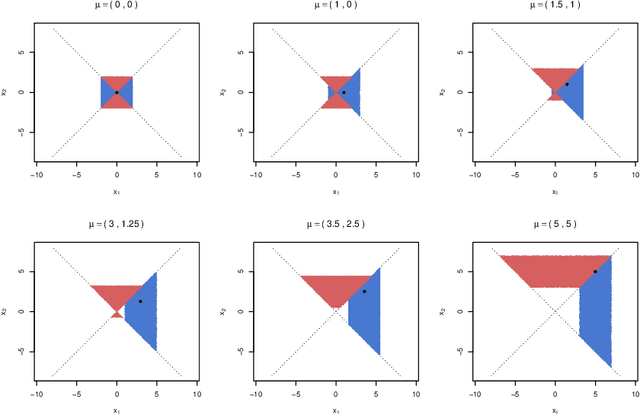
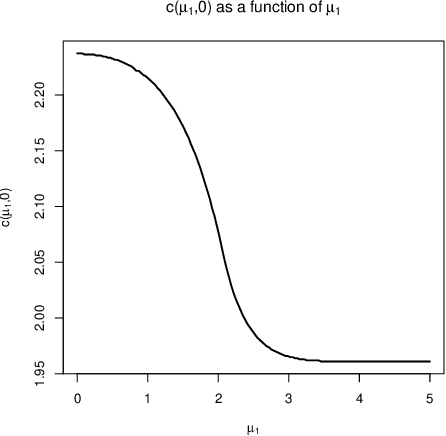
Practical or scientific considerations often lead to selecting a subset of parameters as ``important.'' Inferences about those parameters often are based on the same data used to select them in the first place. That can make the reported uncertainties deceptively optimistic: confidence intervals that ignore selection generally have less than their nominal coverage probability. Controlling the probability that one or more intervals for selected parameters do not cover---the ``simultaneous over the selected'' (SoS) error rate---is crucial in many scientific problems. Intervals that control the SoS error rate can be constructed in ways that take advantage of knowledge of the selection rule. We construct SoS-controlling confidence intervals for parameters deemed the most ``important'' $k$ of $m$ shift parameters because they are estimated (by independent estimators) to be the largest. The new intervals improve substantially over \v{S}id\'{a}k intervals when $k$ is small compared to $m$, and approach the standard Bonferroni-corrected intervals when $k \approx m$. Standard, unadjusted confidence intervals for location parameters have the correct coverage probability for $k=1$, $m=2$ if, when the true parameters are zero, the estimators are exchangeable and symmetric.

Cautious Deep Learning

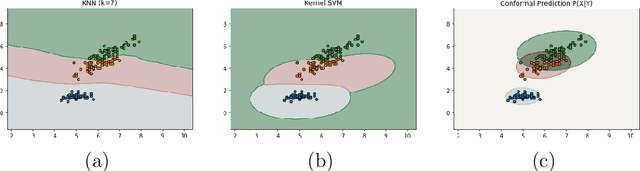
Most classifiers operate by selecting the maximum of an estimate of the conditional distribution $p(y|x)$ where $x$ stands for the features of the instance to be classified and $y$ denotes its label. This often results in a hubristic bias: overconfidence in the assignment of a definite label. Usually, the observations are concentrated on a small volume but the classifier provides definite predictions for the entire space. We propose constructing conformal prediction sets [vovk2005algorithmic] which contain a set of labels rather than a single label. These conformal prediction sets contain the true label with probability $1-\alpha$. Our construction is based on $p(x|y)$ rather than $p(y|x)$ which results in a classifier that is very cautious: it outputs the null set - meaning `I don't know' --- when the object does not resemble the training examples. An important property of our approach is that classes can be added or removed without having to retrain the classifier. We demonstrate the performance on the ImageNet ILSVRC dataset using high dimensional features obtained from state of the art convolutional neural networks.

A Generalization of Convolutional Neural Networks to Graph-Structured Data

This paper introduces a generalization of Convolutional Neural Networks (CNNs) from low-dimensional grid data, such as images, to graph-structured data. We propose a novel spatial convolution utilizing a random walk to uncover the relations within the input, analogous to the way the standard convolution uses the spatial neighborhood of a pixel on the grid. The convolution has an intuitive interpretation, is efficient and scalable and can also be used on data with varying graph structure. Furthermore, this generalization can be applied to many standard regression or classification problems, by learning the the underlying graph. We empirically demonstrate the performance of the proposed CNN on MNIST, and challenge the state-of-the-art on Merck molecular activity data set.

Interpretation of Prediction Models Using the Input Gradient

State of the art machine learning algorithms are highly optimized to provide the optimal prediction possible, naturally resulting in complex models. While these models often outperform simpler more interpretable models by order of magnitudes, in terms of understanding the way the model functions, we are often facing a "black box". In this paper we suggest a simple method to interpret the behavior of any predictive model, both for regression and classification. Given a particular model, the information required to interpret it can be obtained by studying the partial derivatives of the model with respect to the input. We exemplify this insight by interpreting convolutional and multi-layer neural networks in the field of natural language processing.