Yoav Benjamini
Confidence Intervals for Selected Parameters
Jun 02, 2019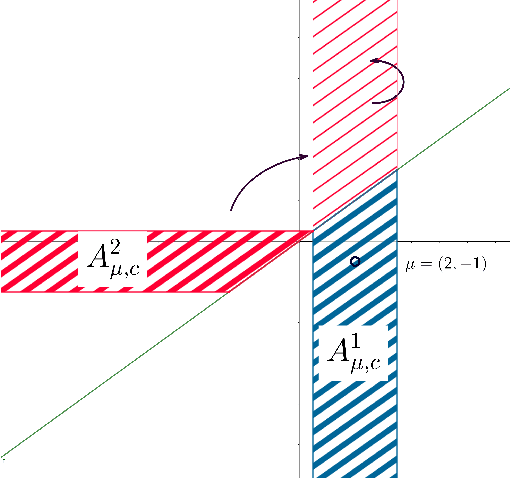
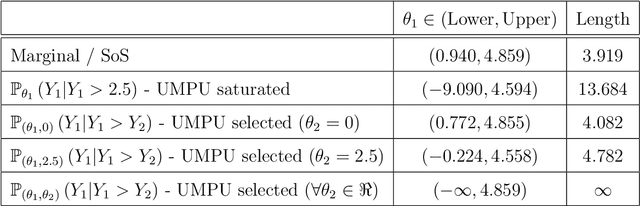
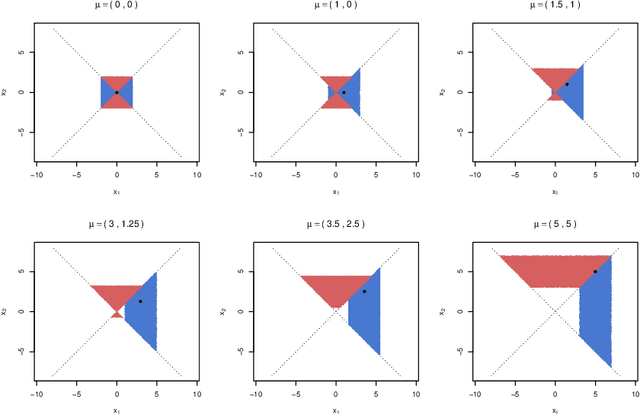
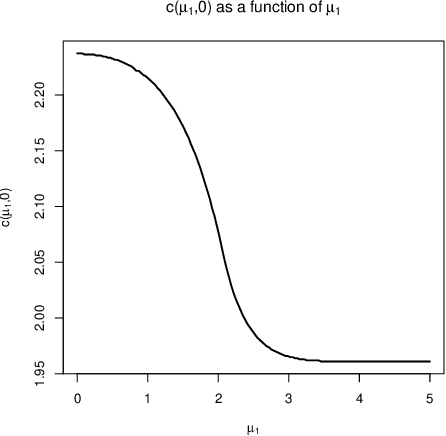
Abstract:Practical or scientific considerations often lead to selecting a subset of parameters as ``important.'' Inferences about those parameters often are based on the same data used to select them in the first place. That can make the reported uncertainties deceptively optimistic: confidence intervals that ignore selection generally have less than their nominal coverage probability. Controlling the probability that one or more intervals for selected parameters do not cover---the ``simultaneous over the selected'' (SoS) error rate---is crucial in many scientific problems. Intervals that control the SoS error rate can be constructed in ways that take advantage of knowledge of the selection rule. We construct SoS-controlling confidence intervals for parameters deemed the most ``important'' $k$ of $m$ shift parameters because they are estimated (by independent estimators) to be the largest. The new intervals improve substantially over \v{S}id\'{a}k intervals when $k$ is small compared to $m$, and approach the standard Bonferroni-corrected intervals when $k \approx m$. Standard, unadjusted confidence intervals for location parameters have the correct coverage probability for $k=1$, $m=2$ if, when the true parameters are zero, the estimators are exchangeable and symmetric.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge