Refined Convergence Rates for Maximum Likelihood Estimation under Finite Mixture Models

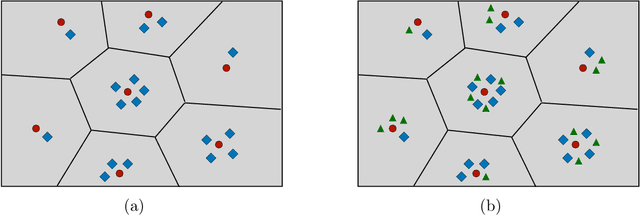
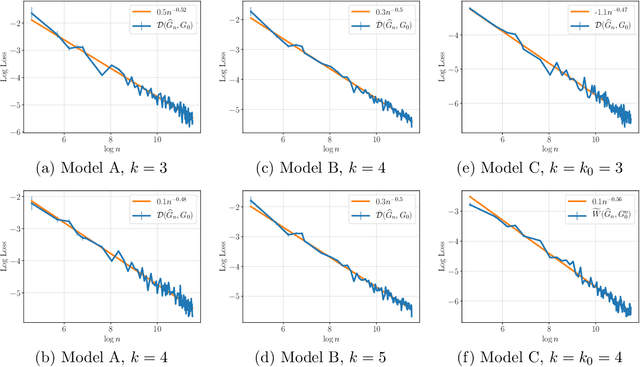
We revisit convergence rates for maximum likelihood estimation (MLE) under finite mixture models. The Wasserstein distance has become a standard loss function for the analysis of parameter estimation in these models, due in part to its ability to circumvent label switching and to accurately characterize the behaviour of fitted mixture components with vanishing weights. However, the Wasserstein metric is only able to capture the worst-case convergence rate among the remaining fitted mixture components. We demonstrate that when the log-likelihood function is penalized to discourage vanishing mixing weights, stronger loss functions can be derived to resolve this shortcoming of the Wasserstein distance. These new loss functions accurately capture the heterogeneity in convergence rates of fitted mixture components, and we use them to sharpen existing pointwise and uniform convergence rates in various classes of mixture models. In particular, these results imply that a subset of the components of the penalized MLE typically converge significantly faster than could have been anticipated from past work. We further show that some of these conclusions extend to the traditional MLE. Our theoretical findings are supported by a simulation study to illustrate these improved convergence rates.

Plugin Estimation of Smooth Optimal Transport Maps

We analyze a number of natural estimators for the optimal transport map between two distributions and show that they are minimax optimal. We adopt the plugin approach: our estimators are simply optimal couplings between measures derived from our observations, appropriately extended so that they define functions on $\mathbb{R}^d$. When the underlying map is assumed to be Lipschitz, we show that computing the optimal coupling between the empirical measures, and extending it using linear smoothers, already gives a minimax optimal estimator. When the underlying map enjoys higher regularity, we show that the optimal coupling between appropriate nonparametric density estimates yields faster rates. Our work also provides new bounds on the risk of corresponding plugin estimators for the quadratic Wasserstein distance, and we show how this problem relates to that of estimating optimal transport maps using stability arguments for smooth and strongly convex Brenier potentials. As an application of our results, we derive a central limit theorem for a density plugin estimator of the squared Wasserstein distance, which is centered at its population counterpart when the underlying distributions have sufficiently smooth densities. In contrast to known central limit theorems for empirical estimators, this result easily lends itself to statistical inference for Wasserstein distances.

Sequential Estimation of Convex Divergences using Reverse Submartingales and Exchangeable Filtrations

We present a unified technique for sequential estimation of convex divergences between distributions, including integral probability metrics like the kernel maximum mean discrepancy, $\varphi$-divergences like the Kullback-Leibler divergence, and optimal transport costs, such as powers of Wasserstein distances. The technical underpinnings of our approach lie in the observation that empirical convex divergences are (partially ordered) reverse submartingales with respect to the exchangeable filtration, coupled with maximal inequalities for such processes. These techniques appear to be powerful additions to the existing literature on both confidence sequences and convex divergences. We construct an offline-to-sequential device that converts a wide array of existing offline concentration inequalities into time-uniform confidence sequences that can be continuously monitored, providing valid inference at arbitrary stopping times. The resulting sequential bounds pay only an iterated logarithmic price over the corresponding fixed-time bounds, retaining the same dependence on problem parameters (like dimension or alphabet size if applicable).

Uniform Convergence Rates for Maximum Likelihood Estimation under Two-Component Gaussian Mixture Models

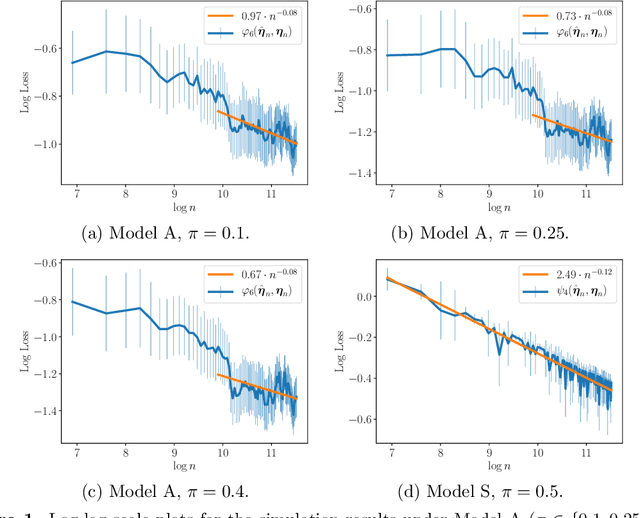
We derive uniform convergence rates for the maximum likelihood estimator and minimax lower bounds for parameter estimation in two-component location-scale Gaussian mixture models with unequal variances. We assume the mixing proportions of the mixture are known and fixed, but make no separation assumption on the underlying mixture components. A phase transition is shown to exist in the optimal parameter estimation rate, depending on whether or not the mixture is balanced. Key to our analysis is a careful study of the dependence between the parameters of location-scale Gaussian mixture models, as captured through systems of polynomial equalities and inequalities whose solution set drives the rates we obtain. A simulation study illustrates the theoretical findings of this work.

Estimating the Number of Components in Finite Mixture Models via the Group-Sort-Fuse Procedure

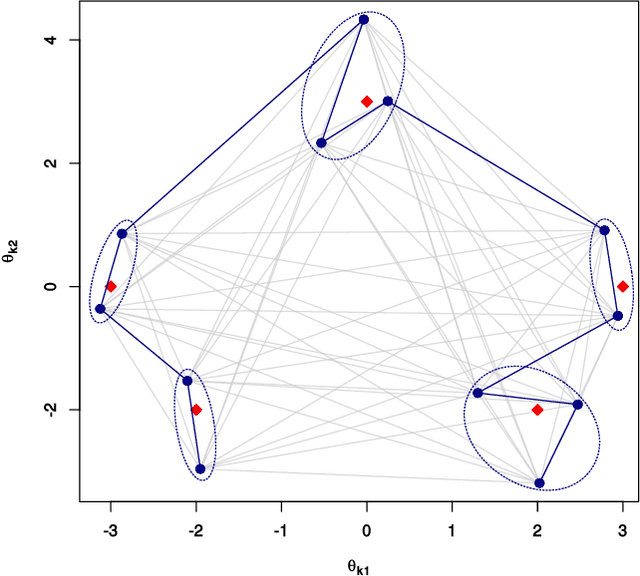
Estimation of the number of components (or order) of a finite mixture model is a long standing and challenging problem in statistics. We propose the Group-Sort-Fuse (GSF) procedure---a new penalized likelihood approach for simultaneous estimation of the order and mixing measure in multidimensional finite mixture models. Unlike methods which fit and compare mixtures with varying orders using criteria involving model complexity, our approach directly penalizes a continuous function of the model parameters. More specifically, given a conservative upper bound on the order, the GSF groups and sorts mixture component parameters to fuse those which are redundant. For a wide range of finite mixture models, we show that the GSF is consistent in estimating the true mixture order and achieves the $n^{-1/2}$ convergence rate for parameter estimation up to polylogarithmic factors. The GSF is implemented for several univariate and multivariate mixture models in the R package GroupSortFuse. Its finite sample performance is supported by a thorough simulation study, and its application is illustrated on two real data examples.

Minimax Confidence Intervals for the Sliced Wasserstein Distance

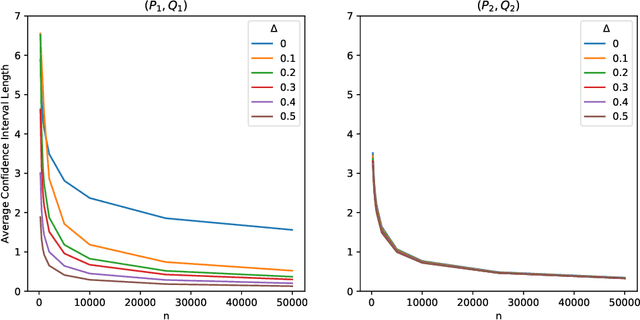
The Wasserstein distance has risen in popularity in the statistics and machine learning communities as a useful metric for comparing probability distributions. We study the problem of uncertainty quantification for the Sliced Wasserstein distance--an easily computable approximation of the Wasserstein distance. Specifically, we construct confidence intervals for the Sliced Wasserstein distance which have finite-sample validity under no assumptions or mild moment assumptions, and are adaptive in length to the smoothness of the underlying distributions. We also bound the minimax risk of estimating the Sliced Wasserstein distance, and show that the length of our proposed confidence intervals is minimax optimal over appropriate distribution classes. To motivate the choice of these classes, we also study minimax rates of estimating a distribution under the Sliced Wasserstein distance. These theoretical findings are complemented with a simulation study.