Understanding Energy Efficiency and Interference Tolerance in Millimeter Wave Receivers

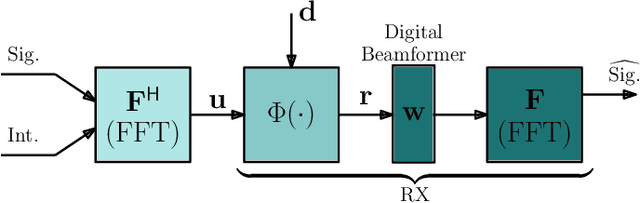
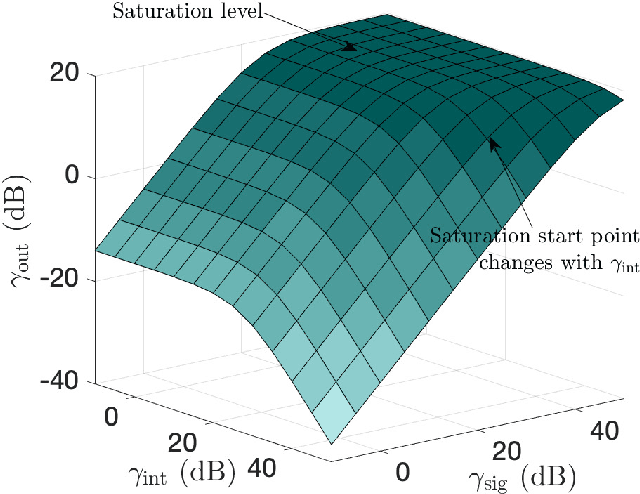
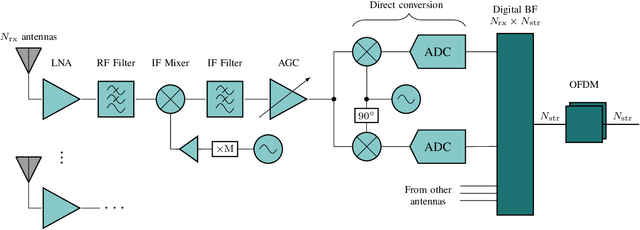
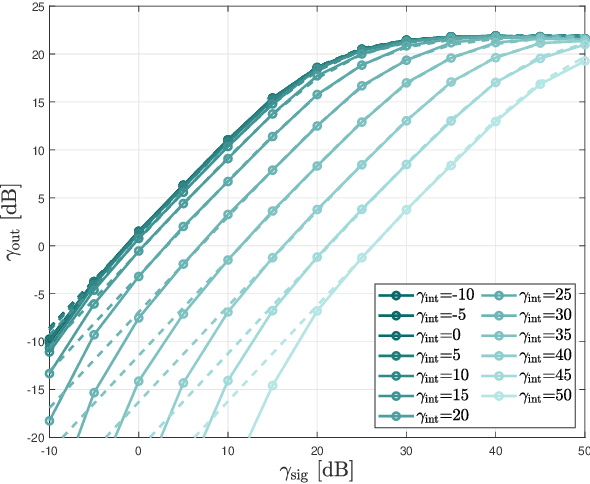
Power consumption is a key challenge in millimeter wave (mmWave) receiver front-ends, due to the need to support high dimensional antenna arrays at wide bandwidths. Recently, there has been considerable work in developing low-power front-ends, often based on low-resolution ADCs and low-power mixers. A critical but less studied consequence of such designs is the relatively low-dynamic range which in turn exposes the receiver to adjacent carrier interference and blockers. This paper provides a general mathematical framework for analyzing the performance of mmWave front-ends in the presence of out-of-band interference. The goal is to elucidate the fundamental trade-off of power consumption, interference tolerance and in-band performance. The analysis is combined with detailed network simulations in cellular systems with multiple carriers, as well as detailed circuit simulations of key components at 140 GHz. The analysis reveals critical bottlenecks for low-power interference robustness and suggests designs enhancements for use in practical systems.

Divide-and-Conquer Hard-thresholding Rules in High-dimensional Imbalanced Classification

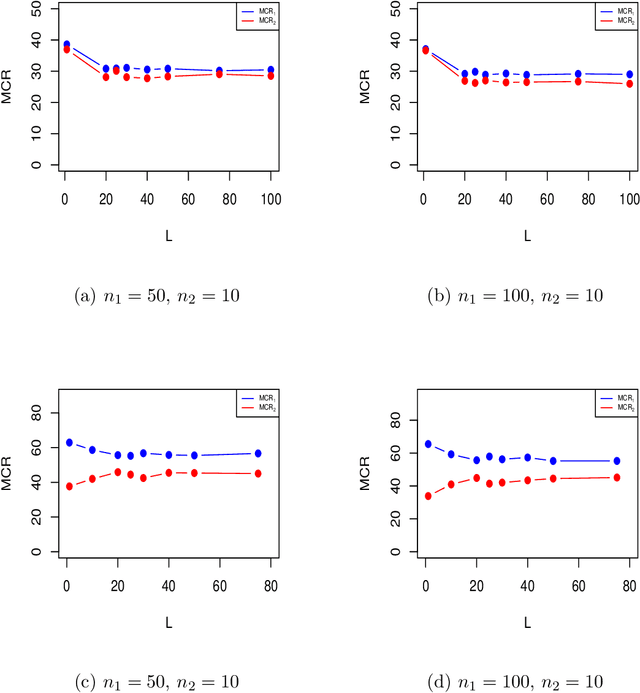
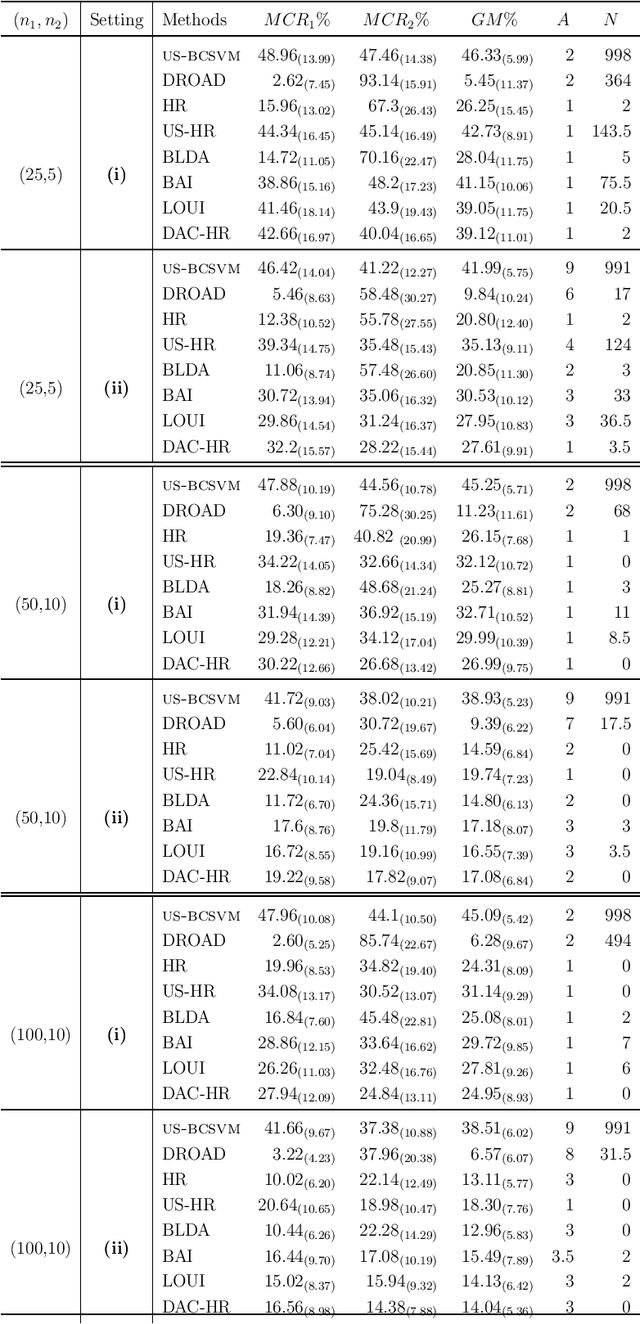
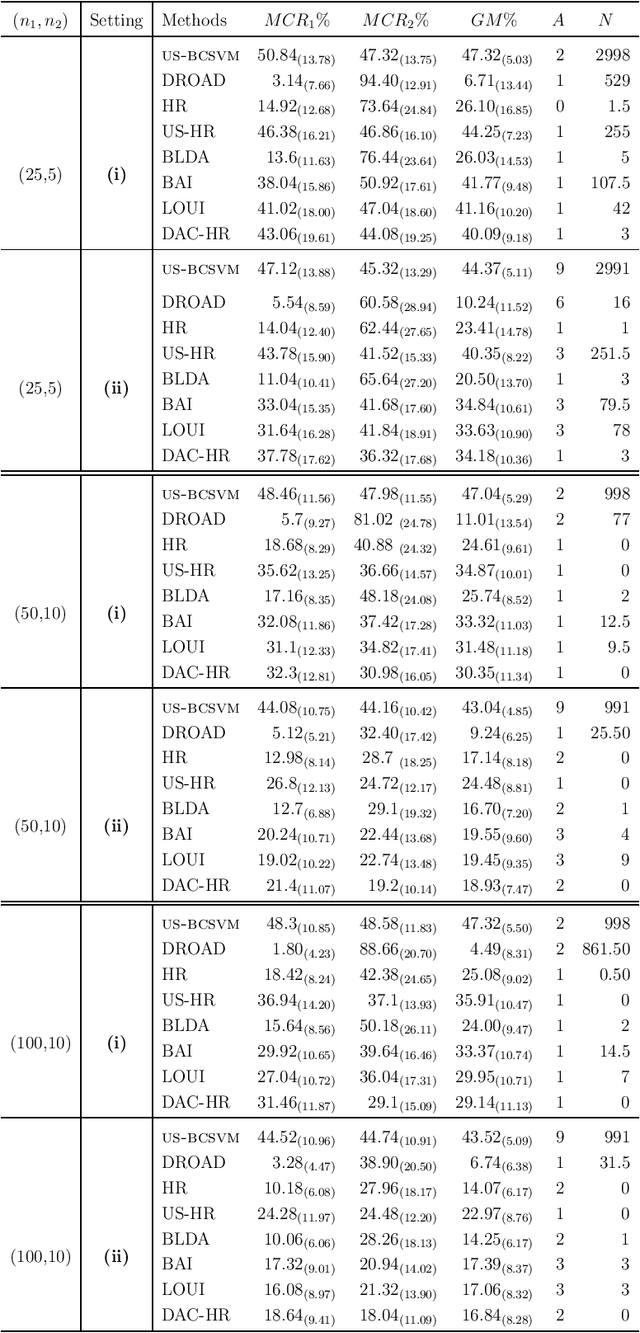
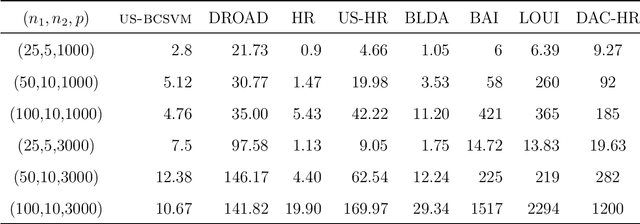
In binary classification, imbalance refers to situations in which one class is heavily under-represented. This issue is due to either a data collection process or because one class is indeed rare in a population. Imbalanced classification frequently arises in applications such as biology, medicine, engineering, and social sciences. In this manuscript, for the first time, we theoretically study the impact of imbalance class sizes on the linear discriminant analysis (LDA) in high dimensions. We show that due to data scarcity in one class, referred to as the minority class, and high-dimensionality of the feature space, the LDA ignores the minority class yielding a maximum misclassification rate. We then propose a new construction of a hard-thresholding rule based on a divide-and-conquer technique that reduces the large difference between the misclassification rates. We show that the proposed method is asymptotically optimal. We further study two well-known sparse versions of the LDA in imbalanced cases. We evaluate the finite-sample performance of different methods using simulations and by analyzing two real data sets. The results show that our method either outperforms its competitors or has comparable performance based on a much smaller subset of selected features, while being computationally more efficient.

On Single-User Interactive Beam Alignment in Next Generation Systems: A Deep Learning Viewpoint

Communication in high frequencies such as millimeter wave and terahertz suffer from high path-loss and intense shadowing which necessitates beamforming for reliable data transmission. On the other hand, at high frequencies the channels are sparse and consist of few spatial clusters. Therefore, beam alignment (BA) strategies are used to find the direction of these channel clusters and adjust the width of the beam used for data transmission. In this work, a single-user uplink scenario where the channel has one dominant cluster is considered. It is assumed that the user transmits a set of BA packets over a fixed duration. Meanwhile, the base-station (BS) uses different probing beams to scan different angular regions. Since the BS measurements are noisy, it is not possible to find a narrow beam that includes the angle of arrival (AoA) of the user with probability one. Therefore, the BS allocates a narrow beam to the user which includes the AoA of the user with a predetermined error probability while minimizing the expected beamwidth of the allocated beam. Due to intractability of this noisy BA problem, here this problem is posed as an end-to-end optimization of a deep neural network (DNN) and effects of different loss functions are discussed and investigated. It is observed that the proposed DNN based BA, at high SNRs, achieves a performance close to that of the optimal BA when there is no-noise and for all SNRs, outperforms state-of-the-art.

Estimating the Number of Components in Finite Mixture Models via the Group-Sort-Fuse Procedure

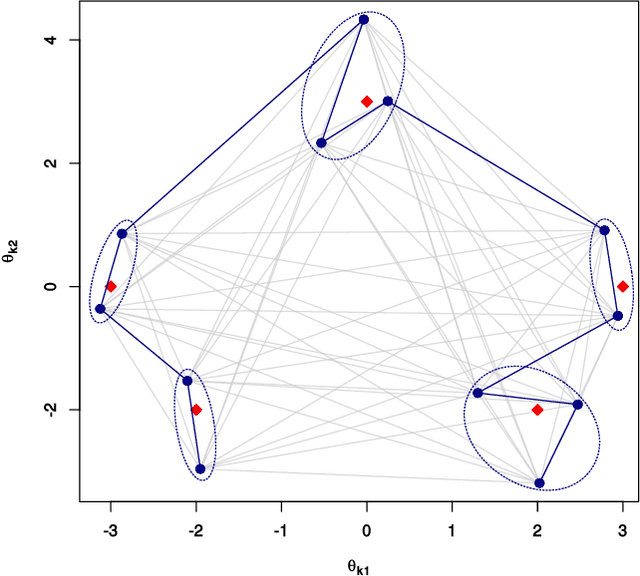
Estimation of the number of components (or order) of a finite mixture model is a long standing and challenging problem in statistics. We propose the Group-Sort-Fuse (GSF) procedure---a new penalized likelihood approach for simultaneous estimation of the order and mixing measure in multidimensional finite mixture models. Unlike methods which fit and compare mixtures with varying orders using criteria involving model complexity, our approach directly penalizes a continuous function of the model parameters. More specifically, given a conservative upper bound on the order, the GSF groups and sorts mixture component parameters to fuse those which are redundant. For a wide range of finite mixture models, we show that the GSF is consistent in estimating the true mixture order and achieves the $n^{-1/2}$ convergence rate for parameter estimation up to polylogarithmic factors. The GSF is implemented for several univariate and multivariate mixture models in the R package GroupSortFuse. Its finite sample performance is supported by a thorough simulation study, and its application is illustrated on two real data examples.