Divide-and-Conquer Hard-thresholding Rules in High-dimensional Imbalanced Classification
Paper and Code
Nov 05, 2021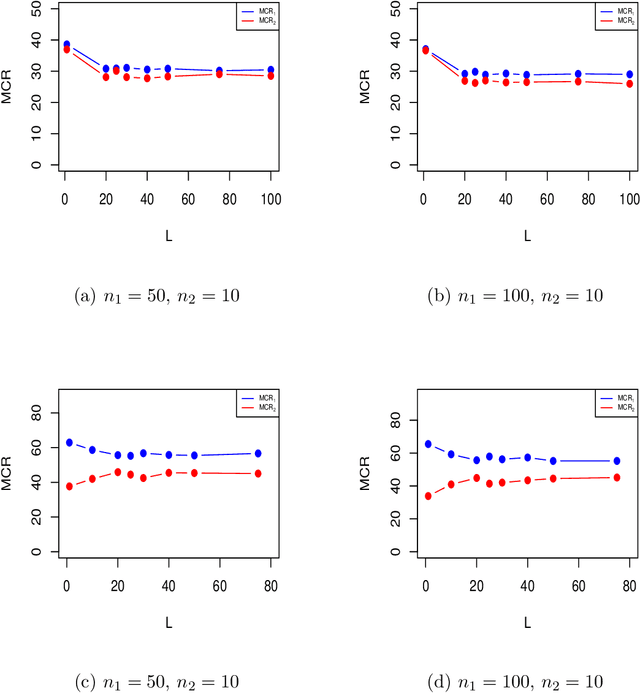
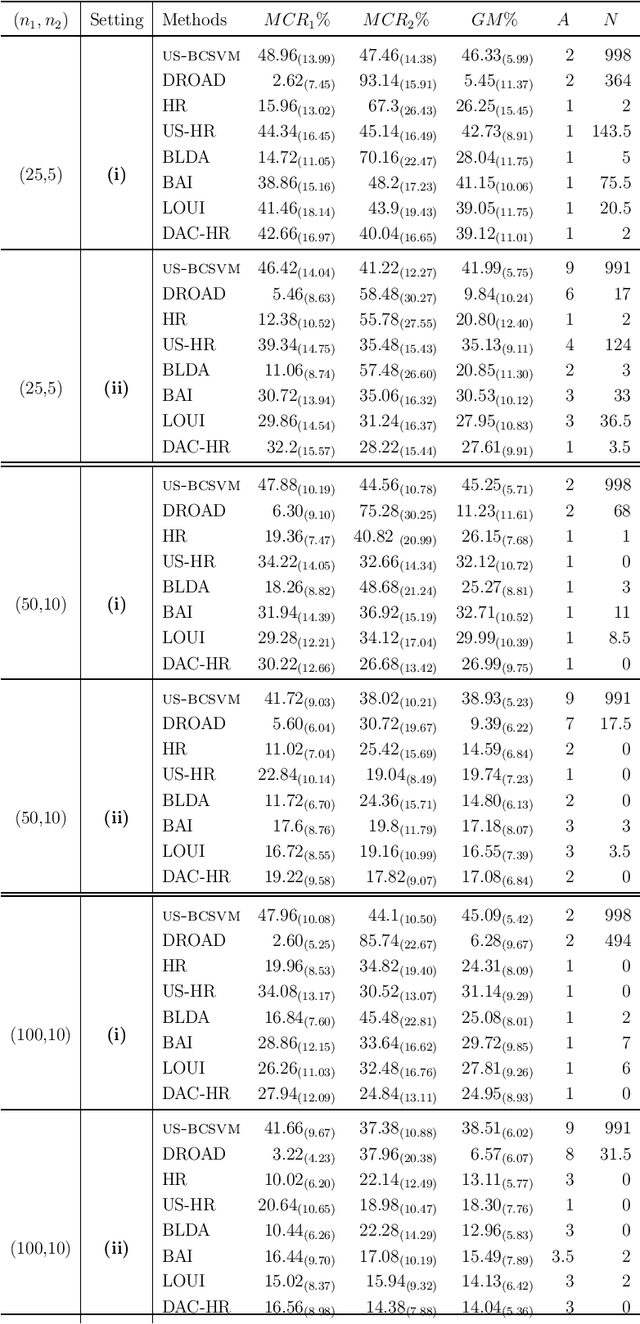
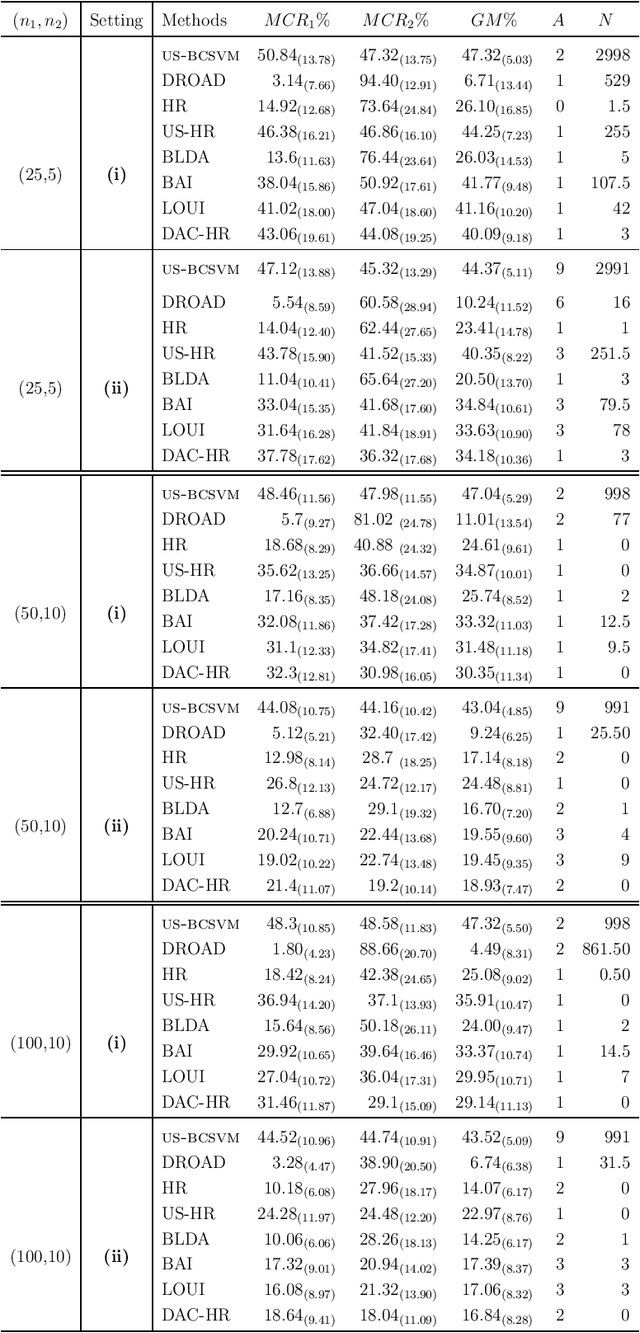
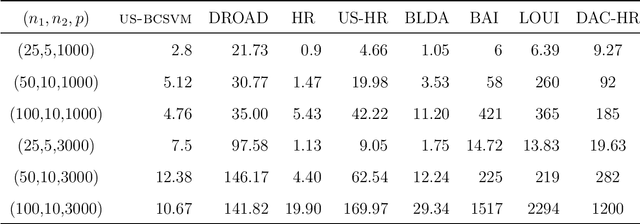
In binary classification, imbalance refers to situations in which one class is heavily under-represented. This issue is due to either a data collection process or because one class is indeed rare in a population. Imbalanced classification frequently arises in applications such as biology, medicine, engineering, and social sciences. In this manuscript, for the first time, we theoretically study the impact of imbalance class sizes on the linear discriminant analysis (LDA) in high dimensions. We show that due to data scarcity in one class, referred to as the minority class, and high-dimensionality of the feature space, the LDA ignores the minority class yielding a maximum misclassification rate. We then propose a new construction of a hard-thresholding rule based on a divide-and-conquer technique that reduces the large difference between the misclassification rates. We show that the proposed method is asymptotically optimal. We further study two well-known sparse versions of the LDA in imbalanced cases. We evaluate the finite-sample performance of different methods using simulations and by analyzing two real data sets. The results show that our method either outperforms its competitors or has comparable performance based on a much smaller subset of selected features, while being computationally more efficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge