Feature Importance: A Closer Look at Shapley Values and LOCO

There is much interest lately in explainability in statistics and machine learning. One aspect of explainability is to quantify the importance of various features (or covariates). Two popular methods for defining variable importance are LOCO (Leave Out COvariates) and Shapley Values. We take a look at the properties of these methods and their advantages and disadvantages. We are particularly interested in the effect of correlation between features which can obscure interpretability. Contrary to some claims, Shapley values do not eliminate feature correlation. We critique the game theoretic axioms for Shapley values and suggest some new axioms. We propose new, more statistically oriented axioms for feature importance and some measures that satisfy these axioms. However, correcting for correlation is a Faustian bargain: removing the effect of correlation creates other forms of bias. Ultimately, we recommend a slightly modified version of LOCO. We briefly consider how to modify Shapley values to better address feature correlation.

Decorrelated Variable Importance

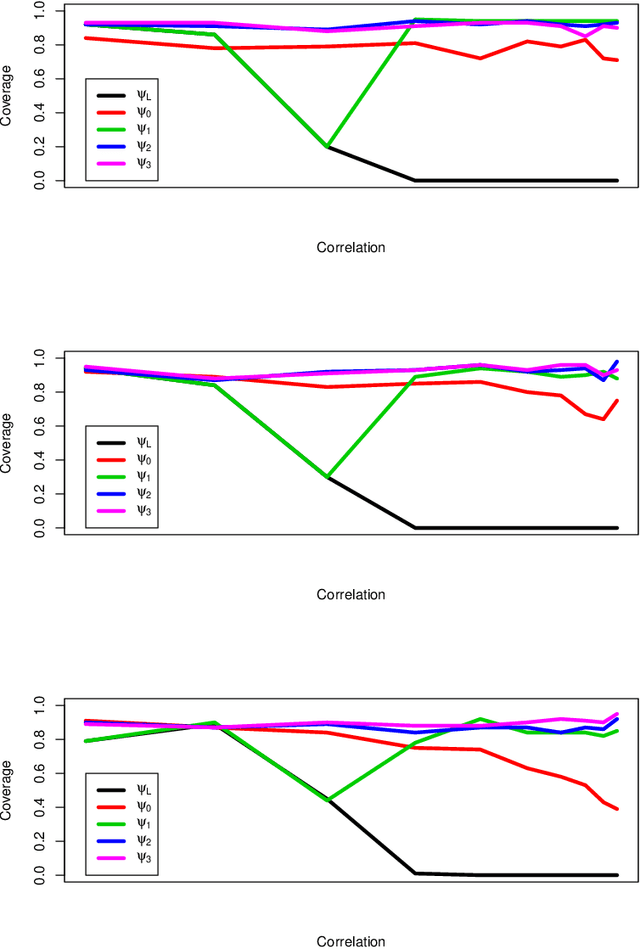
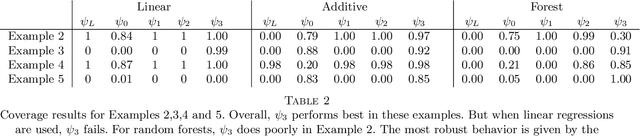
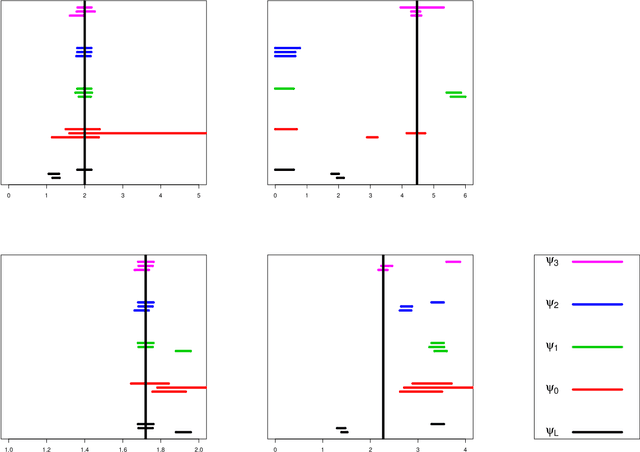
Because of the widespread use of black box prediction methods such as random forests and neural nets, there is renewed interest in developing methods for quantifying variable importance as part of the broader goal of interpretable prediction. A popular approach is to define a variable importance parameter - known as LOCO (Leave Out COvariates) - based on dropping covariates from a regression model. This is essentially a nonparametric version of R-squared. This parameter is very general and can be estimated nonparametrically, but it can be hard to interpret because it is affected by correlation between covariates. We propose a method for mitigating the effect of correlation by defining a modified version of LOCO. This new parameter is difficult to estimate nonparametrically, but we show how to estimate it using semiparametric models.

Forest Guided Smoothing

We use the output of a random forest to define a family of local smoothers with spatially adaptive bandwidth matrices. The smoother inherits the flexibility of the original forest but, since it is a simple, linear smoother, it is very interpretable and it can be used for tasks that would be intractable for the original forest. This includes bias correction, confidence intervals, assessing variable importance and methods for exploring the structure of the forest. We illustrate the method on some synthetic examples and on data related to Covid-19.

Finding Singular Features

We present a method for finding high density, low-dimensional structures in noisy point clouds. These structures are sets with zero Lebesgue measure with respect to the $D$-dimensional ambient space and belong to a $d<D$ dimensional space. We call them "singular features." Hunting for singular features corresponds to finding unexpected or unknown structures hidden in point clouds belonging to $\R^D$. Our method outputs well defined sets of dimensions $d<D$. Unlike spectral clustering, the method works well in the presence of noise. We show how to find singular features by first finding ridges in the estimated density, followed by a filtering step based on the eigenvalues of the Hessian of the density.

Nonparametric ridge estimation

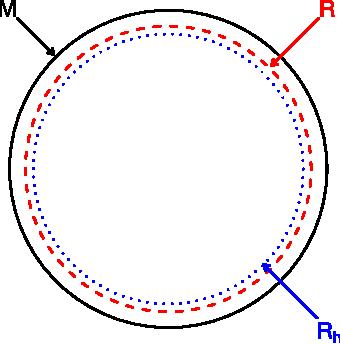
We study the problem of estimating the ridges of a density function. Ridge estimation is an extension of mode finding and is useful for understanding the structure of a density. It can also be used to find hidden structure in point cloud data. We show that, under mild regularity conditions, the ridges of the kernel density estimator consistently estimate the ridges of the true density. When the data are noisy measurements of a manifold, we show that the ridges are close and topologically similar to the hidden manifold. To find the estimated ridges in practice, we adapt the modified mean-shift algorithm proposed by Ozertem and Erdogmus [J. Mach. Learn. Res. 12 (2011) 1249-1286]. Some numerical experiments verify that the algorithm is accurate.

Nonparametric Inference For Density Modes

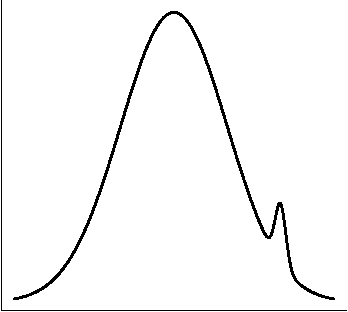
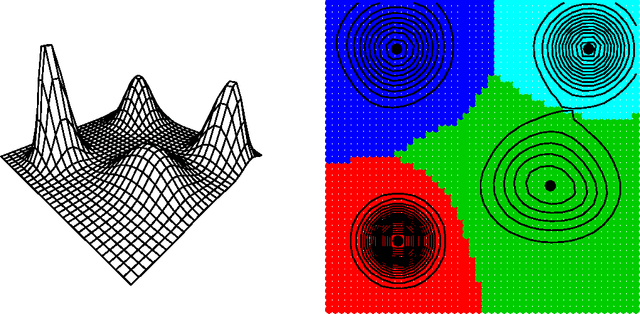
We derive nonparametric confidence intervals for the eigenvalues of the Hessian at modes of a density estimate. This provides information about the strength and shape of modes and can also be used as a significance test. We use a data-splitting approach in which potential modes are identified using the first half of the data and inference is done with the second half of the data. To get valid confidence sets for the eigenvalues, we use a bootstrap based on an elementary-symmetric-polynomial (ESP) transformation. This leads to valid bootstrap confidence sets regardless of any multiplicities in the eigenvalues. We also suggest a new method for bandwidth selection, namely, choosing the bandwidth to maximize the number of significant modes. We show by example that this method works well. Even when the true distribution is singular, and hence does not have a density, (in which case cross validation chooses a zero bandwidth), our method chooses a reasonable bandwidth.

Manifold estimation and singular deconvolution under Hausdorff loss

We find lower and upper bounds for the risk of estimating a manifold in Hausdorff distance under several models. We also show that there are close connections between manifold estimation and the problem of deconvolving a singular measure.

Minimax Manifold Estimation

We find the minimax rate of convergence in Hausdorff distance for estimating a manifold M of dimension d embedded in R^D given a noisy sample from the manifold. We assume that the manifold satisfies a smoothness condition and that the noise distribution has compact support. We show that the optimal rate of convergence is n^{-2/(2+d)}. Thus, the minimax rate depends only on the dimension of the manifold, not on the dimension of the space in which M is embedded.