Nonparametric Inference For Density Modes
Paper and Code
Dec 29, 2013
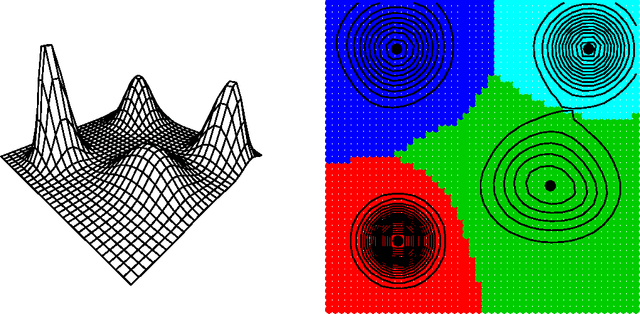

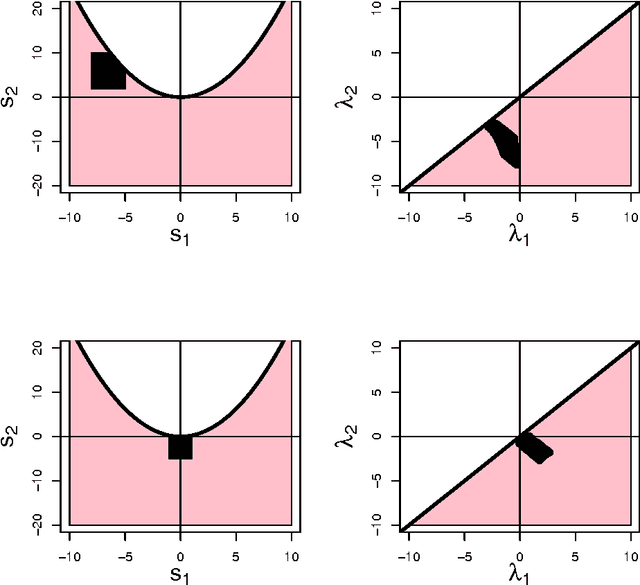
We derive nonparametric confidence intervals for the eigenvalues of the Hessian at modes of a density estimate. This provides information about the strength and shape of modes and can also be used as a significance test. We use a data-splitting approach in which potential modes are identified using the first half of the data and inference is done with the second half of the data. To get valid confidence sets for the eigenvalues, we use a bootstrap based on an elementary-symmetric-polynomial (ESP) transformation. This leads to valid bootstrap confidence sets regardless of any multiplicities in the eigenvalues. We also suggest a new method for bandwidth selection, namely, choosing the bandwidth to maximize the number of significant modes. We show by example that this method works well. Even when the true distribution is singular, and hence does not have a density, (in which case cross validation chooses a zero bandwidth), our method chooses a reasonable bandwidth.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge