Finding Singular Features

We present a method for finding high density, low-dimensional structures in noisy point clouds. These structures are sets with zero Lebesgue measure with respect to the $D$-dimensional ambient space and belong to a $d<D$ dimensional space. We call them "singular features." Hunting for singular features corresponds to finding unexpected or unknown structures hidden in point clouds belonging to $\R^D$. Our method outputs well defined sets of dimensions $d<D$. Unlike spectral clustering, the method works well in the presence of noise. We show how to find singular features by first finding ridges in the estimated density, followed by a filtering step based on the eigenvalues of the Hessian of the density.

The functional mean-shift algorithm for mode hunting and clustering in infinite dimensions

We introduce the functional mean-shift algorithm, an iterative algorithm for estimating the local modes of a surrogate density from functional data. We show that the algorithm can be used for cluster analysis of functional data. We propose a test based on the bootstrap for the significance of the estimated local modes of the surrogate density. We present two applications of our methodology. In the first application, we demonstrate how the functional mean-shift algorithm can be used to perform spike sorting, i.e. cluster neural activity curves. In the second application, we use the functional mean-shift algorithm to distinguish between original and fake signatures.

Estimating the distribution of Galaxy Morphologies on a continuous space

The incredible variety of galaxy shapes cannot be summarized by human defined discrete classes of shapes without causing a possibly large loss of information. Dictionary learning and sparse coding allow us to reduce the high dimensional space of shapes into a manageable low dimensional continuous vector space. Statistical inference can be done in the reduced space via probability distribution estimation and manifold estimation.

Nonparametric Inference For Density Modes

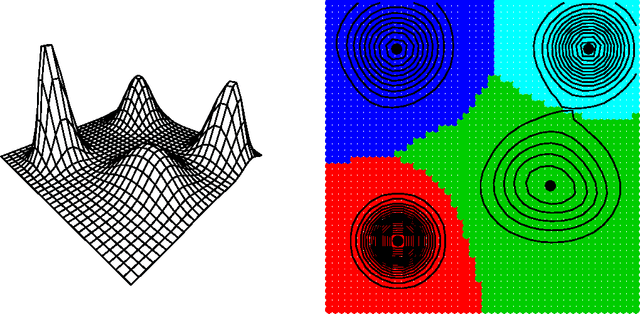
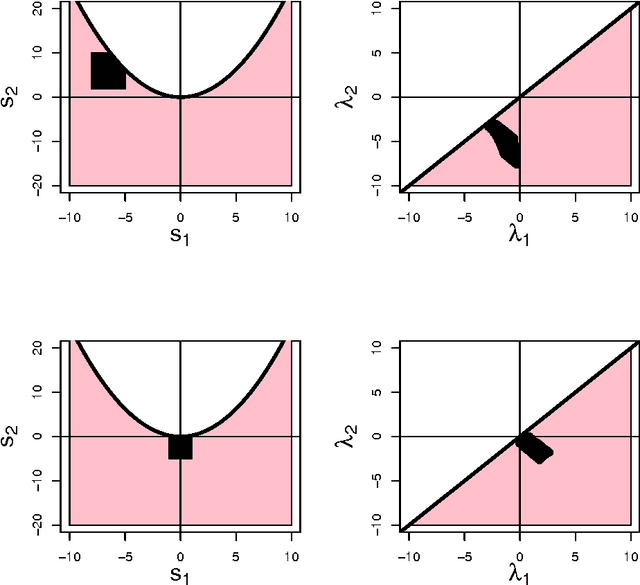
We derive nonparametric confidence intervals for the eigenvalues of the Hessian at modes of a density estimate. This provides information about the strength and shape of modes and can also be used as a significance test. We use a data-splitting approach in which potential modes are identified using the first half of the data and inference is done with the second half of the data. To get valid confidence sets for the eigenvalues, we use a bootstrap based on an elementary-symmetric-polynomial (ESP) transformation. This leads to valid bootstrap confidence sets regardless of any multiplicities in the eigenvalues. We also suggest a new method for bandwidth selection, namely, choosing the bandwidth to maximize the number of significant modes. We show by example that this method works well. Even when the true distribution is singular, and hence does not have a density, (in which case cross validation chooses a zero bandwidth), our method chooses a reasonable bandwidth.

Minimax Manifold Estimation

We find the minimax rate of convergence in Hausdorff distance for estimating a manifold M of dimension d embedded in R^D given a noisy sample from the manifold. We assume that the manifold satisfies a smoothness condition and that the noise distribution has compact support. We show that the optimal rate of convergence is n^{-2/(2+d)}. Thus, the minimax rate depends only on the dimension of the manifold, not on the dimension of the space in which M is embedded.