Statistical Inference using the Morse-Smale Complex

The Morse-Smale complex of a function $f$ decomposes the sample space into cells where $f$ is increasing or decreasing. When applied to nonparametric density estimation and regression, it provides a way to represent, visualize, and compare multivariate functions. In this paper, we present some statistical results on estimating Morse-Smale complexes. This allows us to derive new results for two existing methods: mode clustering and Morse-Smale regression. We also develop two new methods based on the Morse-Smale complex: a visualization technique for multivariate functions and a two-sample, multivariate hypothesis test.

Nonparametric modal regression

Modal regression estimates the local modes of the distribution of $Y$ given $X=x$, instead of the mean, as in the usual regression sense, and can hence reveal important structure missed by usual regression methods. We study a simple nonparametric method for modal regression, based on a kernel density estimate (KDE) of the joint distribution of $Y$ and $X$. We derive asymptotic error bounds for this method, and propose techniques for constructing confidence sets and prediction sets. The latter is used to select the smoothing bandwidth of the underlying KDE. The idea behind modal regression is connected to many others, such as mixture regression and density ridge estimation, and we discuss these ties as well.

A Comprehensive Approach to Mode Clustering

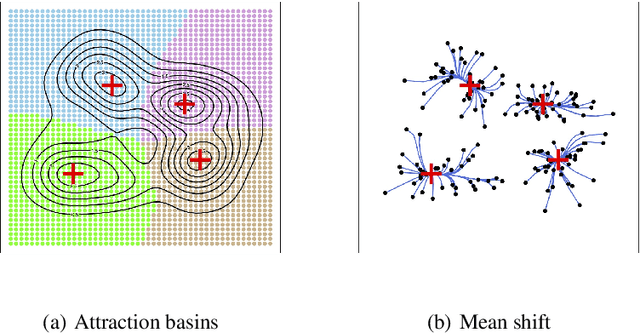
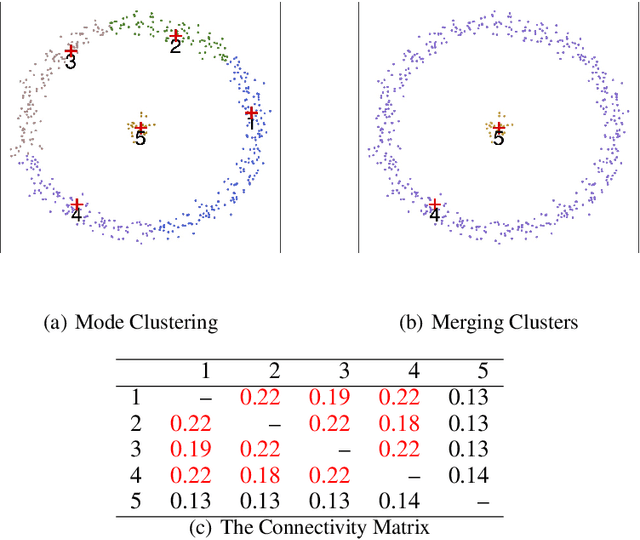
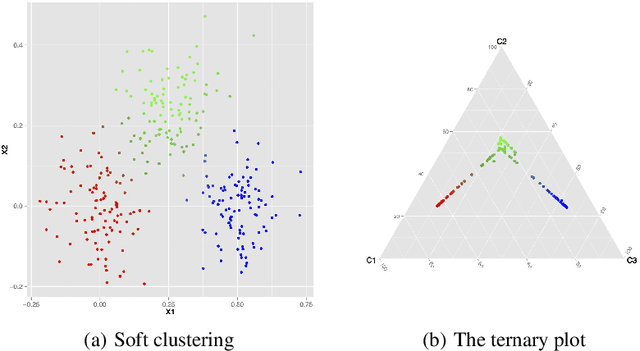
Mode clustering is a nonparametric method for clustering that defines clusters using the basins of attraction of a density estimator's modes. We provide several enhancements to mode clustering: (i) a soft variant of cluster assignment, (ii) a measure of connectivity between clusters, (iii) a technique for choosing the bandwidth, (iv) a method for denoising small clusters, and (v) an approach to visualizing the clusters. Combining all these enhancements gives us a complete procedure for clustering in multivariate problems. We also compare mode clustering to other clustering methods in several examples

Optimal Ridge Detection using Coverage Risk

We introduce the concept of coverage risk as an error measure for density ridge estimation. The coverage risk generalizes the mean integrated square error to set estimation. We propose two risk estimators for the coverage risk and we show that we can select tuning parameters by minimizing the estimated risk. We study the rate of convergence for coverage risk and prove consistency of the risk estimators. We apply our method to three simulated datasets and to cosmology data. In all the examples, the proposed method successfully recover the underlying density structure.

Nonparametric ridge estimation

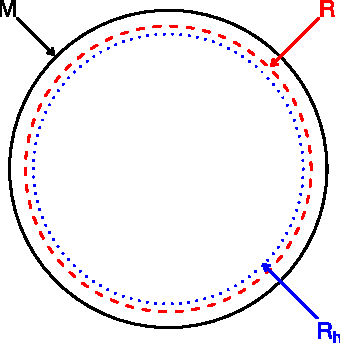
We study the problem of estimating the ridges of a density function. Ridge estimation is an extension of mode finding and is useful for understanding the structure of a density. It can also be used to find hidden structure in point cloud data. We show that, under mild regularity conditions, the ridges of the kernel density estimator consistently estimate the ridges of the true density. When the data are noisy measurements of a manifold, we show that the ridges are close and topologically similar to the hidden manifold. To find the estimated ridges in practice, we adapt the modified mean-shift algorithm proposed by Ozertem and Erdogmus [J. Mach. Learn. Res. 12 (2011) 1249-1286]. Some numerical experiments verify that the algorithm is accurate.

Manifold estimation and singular deconvolution under Hausdorff loss

We find lower and upper bounds for the risk of estimating a manifold in Hausdorff distance under several models. We also show that there are close connections between manifold estimation and the problem of deconvolving a singular measure.