Spatiotemporal Density Correction of Multivariate Global Climate Model Projections using Deep Learning

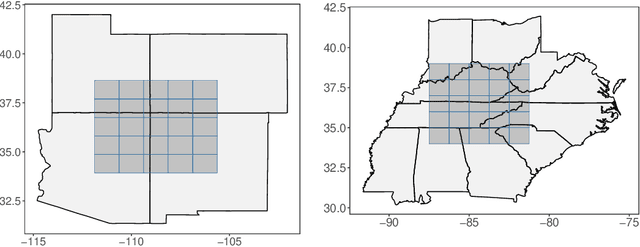
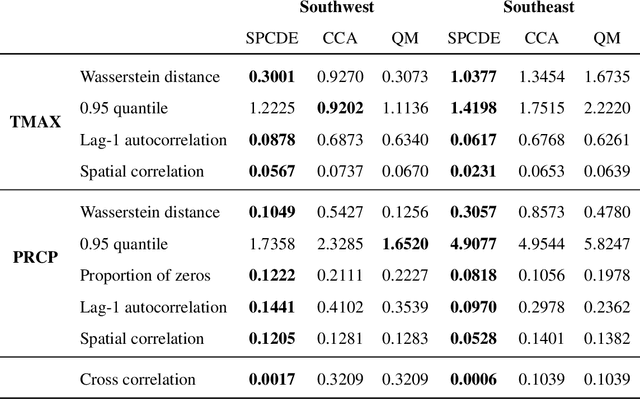
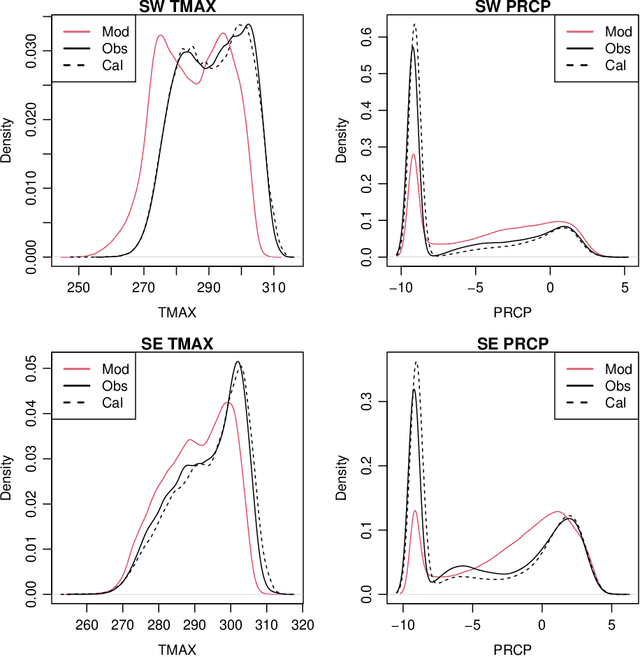
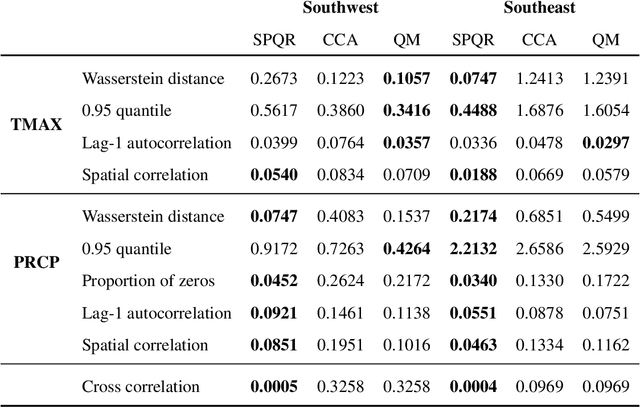
Global Climate Models (GCMs) are numerical models that simulate complex physical processes within the Earth's climate system and are essential for understanding and predicting climate change. However, GCMs suffer from systemic biases due to simplifications made to the underlying physical processes. GCM output therefore needs to be bias corrected before it can be used for future climate projections. Most common bias correction methods, however, cannot preserve spatial, temporal, or inter-variable dependencies. We propose a new semi-parametric conditional density estimation (SPCDE) for density correction of the joint distribution of daily precipitation and maximum temperature data obtained from gridded GCM spatial fields. The Vecchia approximation is employed to preserve dependencies in the observed field during the density correction process, which is carried out using semi-parametric quantile regression. The ability to calibrate joint distributions of GCM projections has potential advantages not only in estimating extremes, but also in better estimating compound hazards, like heat waves and drought, under potential climate change. Illustration on historical data from 1951-2014 over two 5x5 spatial grids in the US indicate that SPCDE can preserve key marginal and joint distribution properties of precipitation and maximum temperature, and predictions obtained using SPCDE are better calibrated compared to predictions using asynchronous quantile mapping and canonical correlation analysis, two commonly used bias correction approaches.

Multivariate and Online Transfer Learning with Uncertainty Quantification

Untreated periodontitis causes inflammation within the supporting tissue of the teeth and can ultimately lead to tooth loss. Modeling periodontal outcomes is beneficial as they are difficult and time consuming to measure, but disparities in representation between demographic groups must be considered. There may not be enough participants to build group specific models and it can be ineffective, and even dangerous, to apply a model to participants in an underrepresented group if demographic differences were not considered during training. We propose an extension to RECaST Bayesian transfer learning framework. Our method jointly models multivariate outcomes, exhibiting significant improvement over the previous univariate RECaST method. Further, we introduce an online approach to model sequential data sets. Negative transfer is mitigated to ensure that the information shared from the other demographic groups does not negatively impact the modeling of the underrepresented participants. The Bayesian framework naturally provides uncertainty quantification on predictions. Especially important in medical applications, our method does not share data between domains. We demonstrate the effectiveness of our method in both predictive performance and uncertainty quantification on simulated data and on a database of dental records from the HealthPartners Institute.

Amortized Bayesian Local Interpolation NetworK: Fast covariance parameter estimation for Gaussian Processes

Gaussian processes (GPs) are a ubiquitous tool for geostatistical modeling with high levels of flexibility and interpretability, and the ability to make predictions at unseen spatial locations through a process called Kriging. Estimation of Kriging weights relies on the inversion of the process' covariance matrix, creating a computational bottleneck for large spatial datasets. In this paper, we propose an Amortized Bayesian Local Interpolation NetworK (A-BLINK) for fast covariance parameter estimation, which uses two pre-trained deep neural networks to learn a mapping from spatial location coordinates and covariance function parameters to Kriging weights and the spatial variance, respectively. The fast prediction time of these networks allows us to bypass the matrix inversion step, creating large computational speedups over competing methods in both frequentist and Bayesian settings, and also provides full posterior inference and predictions using Markov chain Monte Carlo sampling methods. We show significant increases in computational efficiency over comparable scalable GP methodology in an extensive simulation study with lower parameter estimation error. The efficacy of our approach is also demonstrated using a temperature dataset of US climate normals for 1991--2020 based on over 7,000 weather stations.

A variational neural Bayes framework for inference on intractable posterior distributions

Classic Bayesian methods with complex models are frequently infeasible due to an intractable likelihood. Simulation-based inference methods, such as Approximate Bayesian Computing (ABC), calculate posteriors without accessing a likelihood function by leveraging the fact that data can be quickly simulated from the model, but converge slowly and/or poorly in high-dimensional settings. In this paper, we propose a framework for Bayesian posterior estimation by mapping data to posteriors of parameters using a neural network trained on data simulated from the complex model. Posterior distributions of model parameters are efficiently obtained by feeding observed data into the trained neural network. We show theoretically that our posteriors converge to the true posteriors in Kullback-Leibler divergence. Our approach yields computationally efficient and theoretically justified uncertainty quantification, which is lacking in existing simulation-based neural network approaches. Comprehensive simulation studies highlight our method's robustness and accuracy.

A Bayesian Semiparametric Method For Estimating Causal Quantile Effects

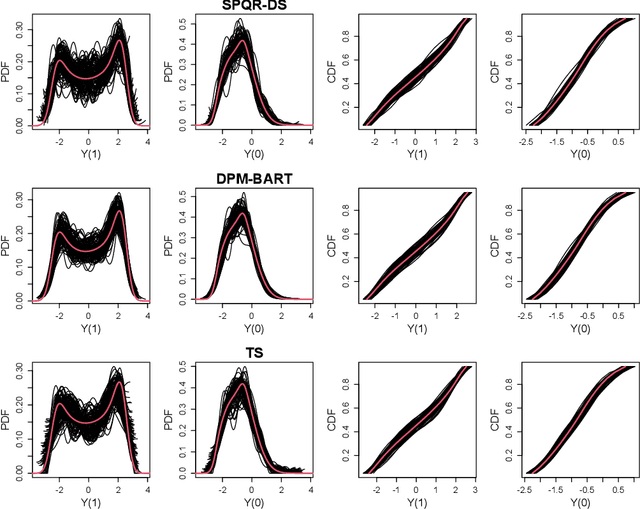
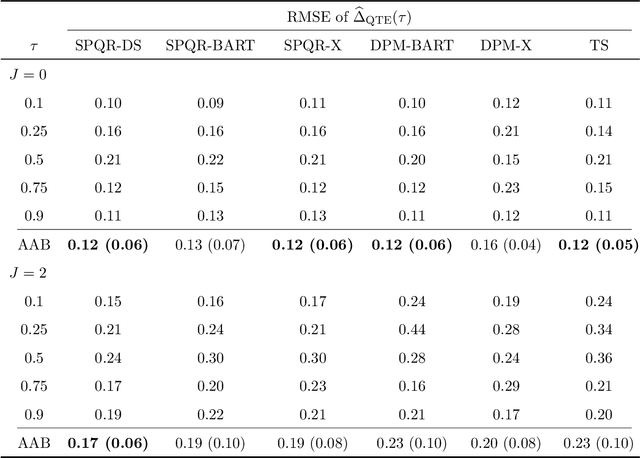
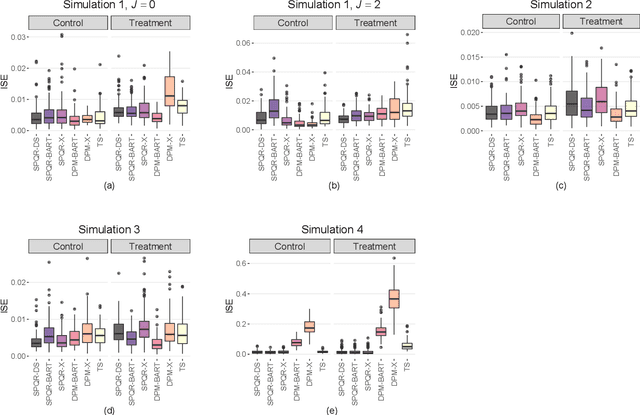
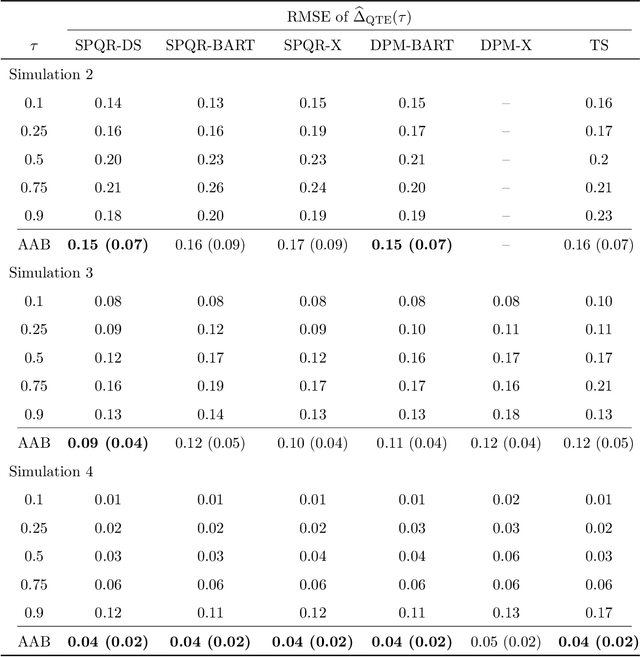
Standard causal inference characterizes treatment effect through averages, but the counterfactual distributions could be different in not only the central tendency but also spread and shape. To provide a comprehensive evaluation of treatment effects, we focus on estimating quantile treatment effects (QTEs). Existing methods that invert a nonsmooth estimator of the cumulative distribution functions forbid inference on probability density functions (PDFs), but PDFs can reveal more nuanced characteristics of the counterfactual distributions. We adopt a semiparametric conditional distribution regression model that allows inference on any functionals of counterfactual distributions, including PDFs and multiple QTEs. To account for the observational nature of the data and ensure an efficient model, we adjust for a double balancing score that augments the propensity score with individual covariates. We provide a Bayesian estimation framework that appropriately propagates modeling uncertainty. We show via simulations that the use of double balancing score for confounding adjustment improves performance over adjusting for any single score alone, and the proposed semiparametric model estimates QTEs more accurately than other semiparametric methods. We apply the proposed method to the North Carolina birth weight dataset to analyze the effect of maternal smoking on infant's birth weight.

SPQR: An R Package for Semi-Parametric Density and Quantile Regression

We develop an R package SPQR that implements the semi-parametric quantile regression (SPQR) method in Xu and Reich (2021). The method begins by fitting a flexible density regression model using monotonic splines whose weights are modeled as data-dependent functions using artificial neural networks. Subsequently, estimates of conditional density and quantile process can all be obtained. Unlike many approaches to quantile regression that assume a linear model, SPQR allows for virtually any relationship between the covariates and the response distribution including non-linear effects and different effects on different quantile levels. To increase the interpretability and transparency of SPQR, model-agnostic statistics developed by Apley and Zhu (2020) are used to estimate and visualize the covariate effects and their relative importance on the quantile function. In this article, we detail how this framework is implemented in SPQR and illustrate how this package should be used in practice through simulated and real data examples.

Nonparametric Conditional Density Estimation In A Deep Learning Framework For Short-Term Forecasting

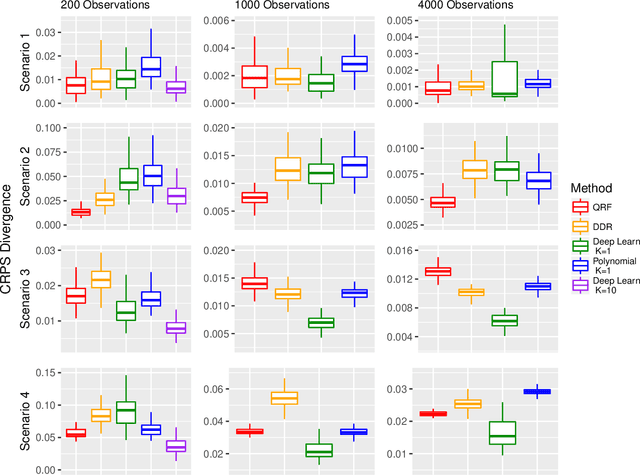
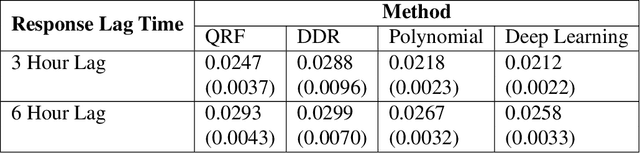
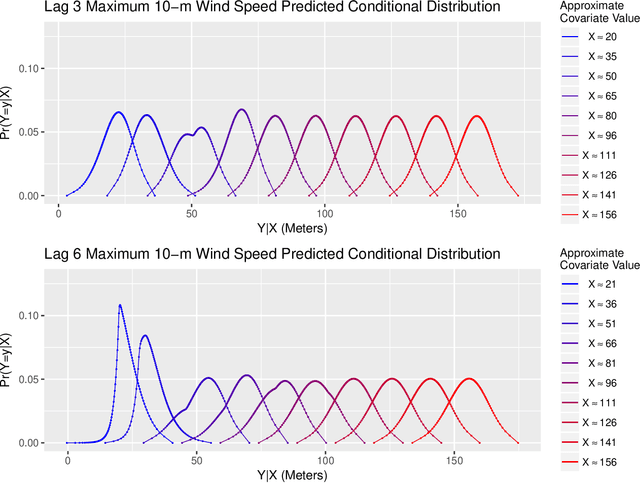
Short-term forecasting is an important tool in understanding environmental processes. In this paper, we incorporate machine learning algorithms into a conditional distribution estimator for the purposes of forecasting tropical cyclone intensity. Many machine learning techniques give a single-point prediction of the conditional distribution of the target variable, which does not give a full accounting of the prediction variability. Conditional distribution estimation can provide extra insight on predicted response behavior, which could influence decision-making and policy. We propose a technique that simultaneously estimates the entire conditional distribution and flexibly allows for machine learning techniques to be incorporated. A smooth model is fit over both the target variable and covariates, and a logistic transformation is applied on the model output layer to produce an expression of the conditional density function. We provide two examples of machine learning models that can be used, polynomial regression and deep learning models. To achieve computational efficiency we propose a case-control sampling approximation to the conditional distribution. A simulation study for four different data distributions highlights the effectiveness of our method compared to other machine learning-based conditional distribution estimation techniques. We then demonstrate the utility of our approach for forecasting purposes using tropical cyclone data from the Atlantic Seaboard. This paper gives a proof of concept for the promise of our method, further computational developments can fully unlock its insights in more complex forecasting and other applications.

Multi-Model Penalized Regression

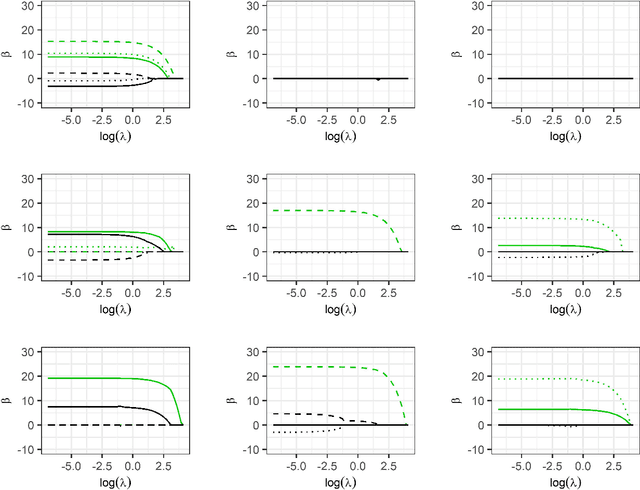
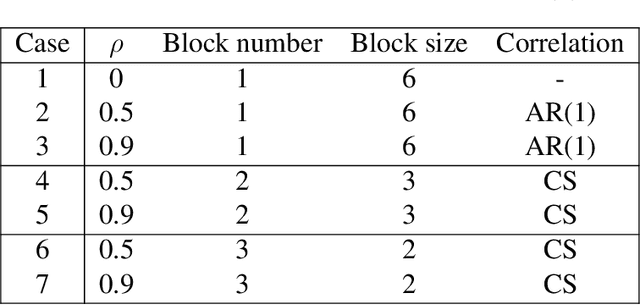
Model fitting often aims to fit a single model, assuming that the imposed form of the model is correct. However, there may be multiple possible underlying explanatory patterns in a set of predictors that could explain a response. Model selection without regarding model uncertainty can fail to bring these patterns to light. We present multi-model penalized regression (MMPR) to acknowledge model uncertainty in the context of penalized regression. In the penalty form introduced here, we explore how different settings can promote either shrinkage or sparsity of coefficients in separate models. A choice of penalty form that enforces variable selection is applied to predict stacking force energy (SFE) from steel alloy composition. The aim is to identify multiple models with different subsets of covariates that explain a single type of response.

Global forensic geolocation with deep neural networks

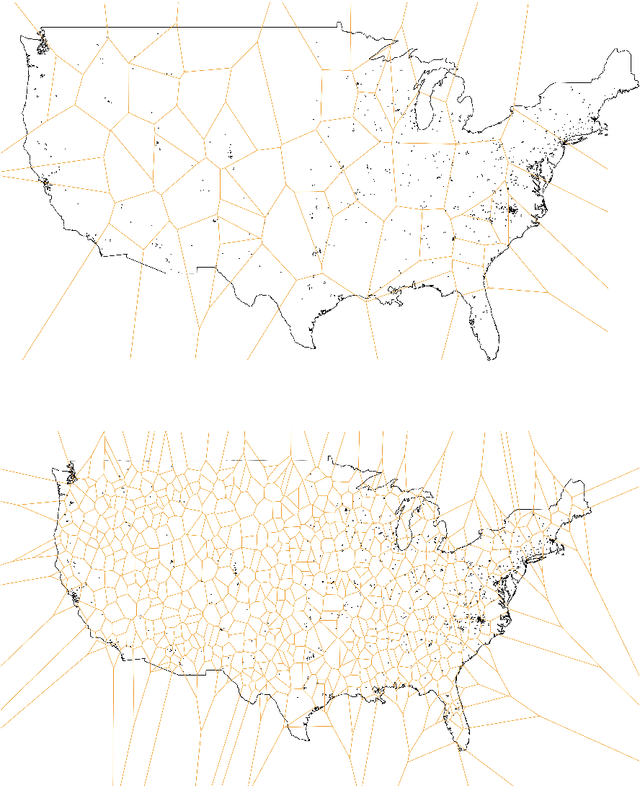
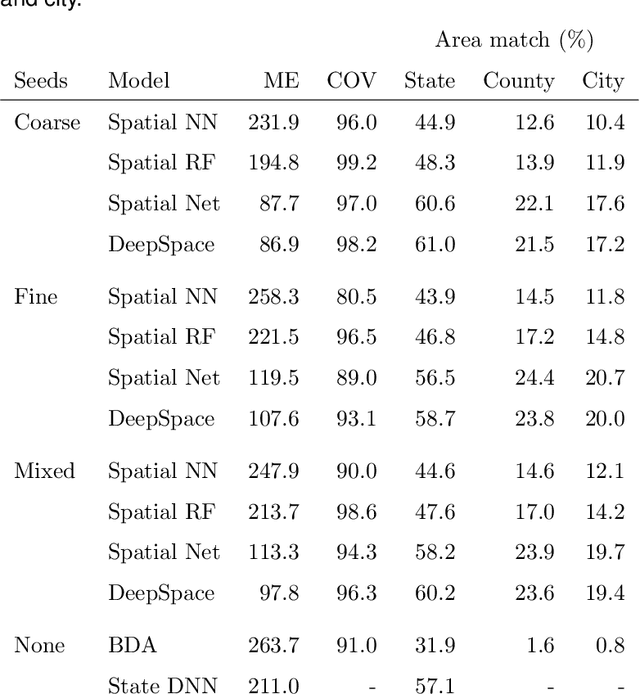
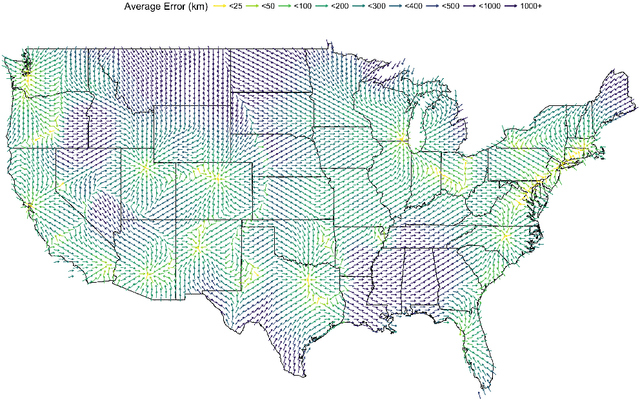
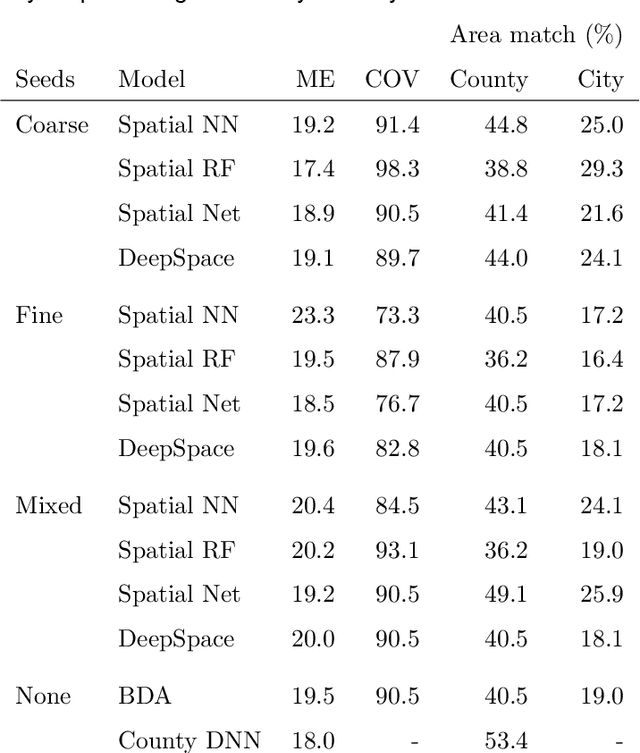
An important problem in forensic analyses is identifying the provenance of materials at a crime scene, such as biological material on a piece of clothing. This procedure, known as geolocation, is conventionally guided by expert knowledge of the biological evidence and therefore tends to be application-specific, labor-intensive, and subjective. Purely data-driven methods have yet to be fully realized due in part to the lack of a sufficiently rich data source. However, high-throughput sequencing technologies are able to identify tens of thousands of microbial taxa using DNA recovered from a single swab collected from nearly any object or surface. We present a new algorithm for geolocation that aggregates over an ensemble of deep neural network classifiers trained on randomly-generated Voronoi partitions of a spatial domain. We apply the algorithm to fungi present in each of 1300 dust samples collected across the continental United States and then to a global dataset of dust samples from 28 countries. Our algorithm makes remarkably good point predictions with more than half of the geolocation errors under 100 kilometers for the continental analysis and nearly 90% classification accuracy of a sample's country of origin for the global analysis. We suggest that the effectiveness of this model sets the stage for a new, quantitative approach to forensic geolocation.

Deep Distribution Regression

Due to their flexibility and predictive performance, machine-learning based regression methods have become an important tool for predictive modeling and forecasting. However, most methods focus on estimating the conditional mean or specific quantiles of the target quantity and do not provide the full conditional distribution, which contains uncertainty information that might be crucial for decision making. In this article, we provide a general solution by transforming a conditional distribution estimation problem into a constrained multi-class classification problem, in which tools such as deep neural networks. We propose a novel joint binary cross-entropy loss function to accomplish this goal. We demonstrate its performance in various simulation studies comparing to state-of-the-art competing methods. Additionally, our method shows improved accuracy in a probabilistic solar energy forecasting problem.