A Bayesian Semiparametric Method For Estimating Causal Quantile Effects
Paper and Code
Nov 03, 2022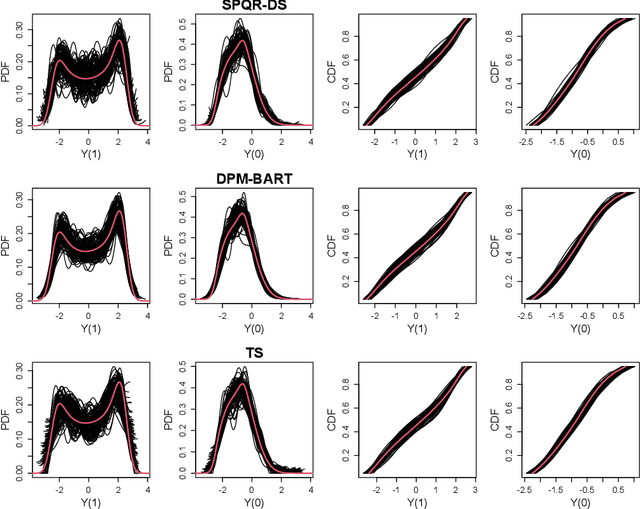
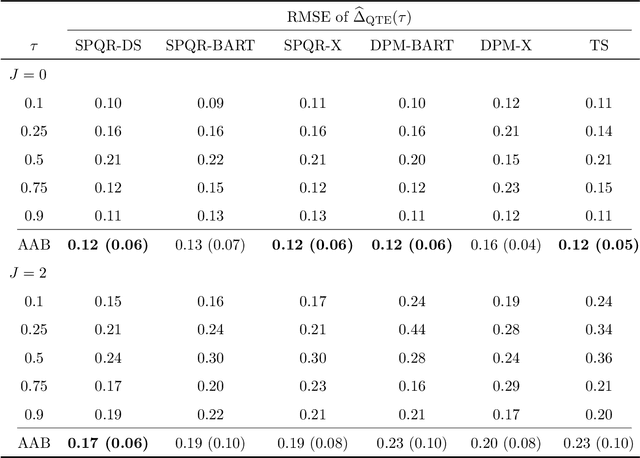
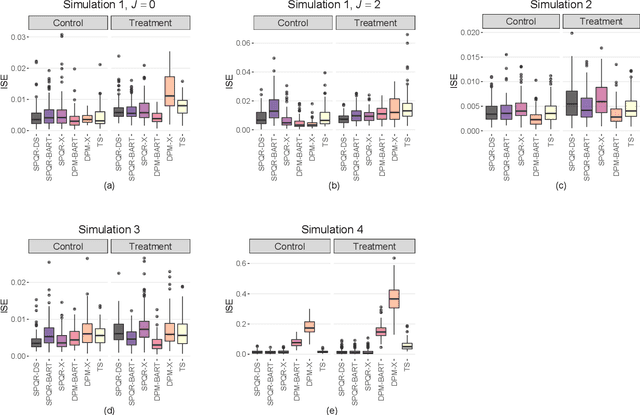
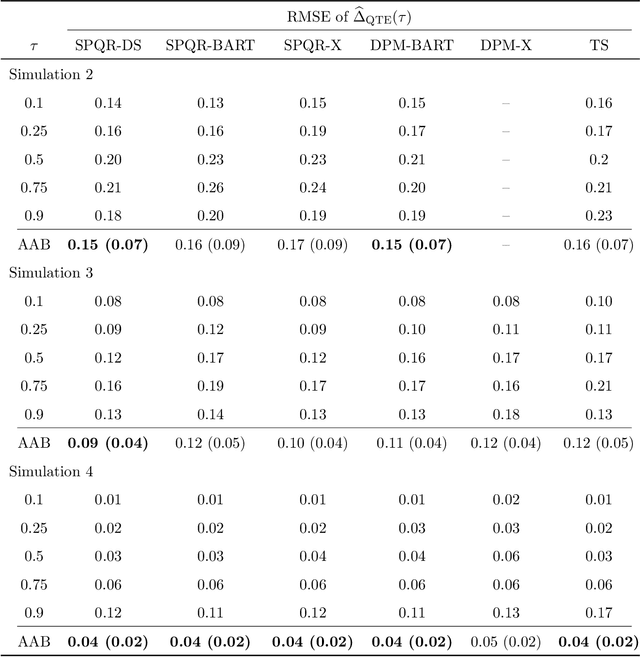
Standard causal inference characterizes treatment effect through averages, but the counterfactual distributions could be different in not only the central tendency but also spread and shape. To provide a comprehensive evaluation of treatment effects, we focus on estimating quantile treatment effects (QTEs). Existing methods that invert a nonsmooth estimator of the cumulative distribution functions forbid inference on probability density functions (PDFs), but PDFs can reveal more nuanced characteristics of the counterfactual distributions. We adopt a semiparametric conditional distribution regression model that allows inference on any functionals of counterfactual distributions, including PDFs and multiple QTEs. To account for the observational nature of the data and ensure an efficient model, we adjust for a double balancing score that augments the propensity score with individual covariates. We provide a Bayesian estimation framework that appropriately propagates modeling uncertainty. We show via simulations that the use of double balancing score for confounding adjustment improves performance over adjusting for any single score alone, and the proposed semiparametric model estimates QTEs more accurately than other semiparametric methods. We apply the proposed method to the North Carolina birth weight dataset to analyze the effect of maternal smoking on infant's birth weight.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge