Eric B. Laber
Sequential Knockoffs for Variable Selection in Reinforcement Learning
Mar 24, 2023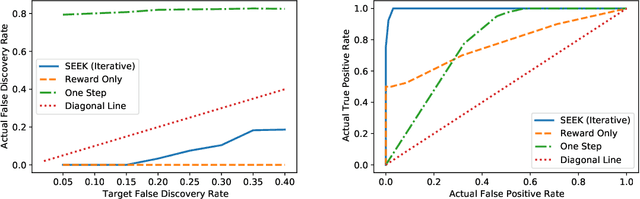


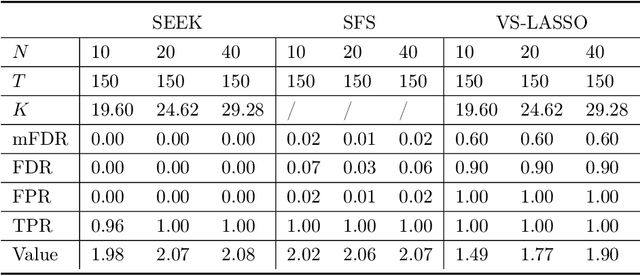
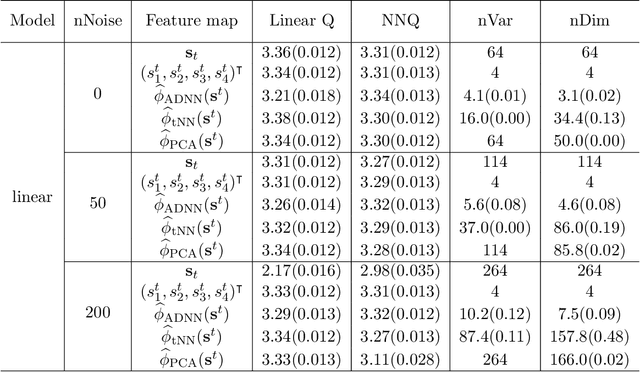
Abstract:In real-world applications of reinforcement learning, it is often challenging to obtain a state representation that is parsimonious and satisfies the Markov property without prior knowledge. Consequently, it is common practice to construct a state which is larger than necessary, e.g., by concatenating measurements over contiguous time points. However, needlessly increasing the dimension of the state can slow learning and obfuscate the learned policy. We introduce the notion of a minimal sufficient state in a Markov decision process (MDP) as the smallest subvector of the original state under which the process remains an MDP and shares the same optimal policy as the original process. We propose a novel sequential knockoffs (SEEK) algorithm that estimates the minimal sufficient state in a system with high-dimensional complex nonlinear dynamics. In large samples, the proposed method controls the false discovery rate, and selects all sufficient variables with probability approaching one. As the method is agnostic to the reinforcement learning algorithm being applied, it benefits downstream tasks such as policy optimization. Empirical experiments verify theoretical results and show the proposed approach outperforms several competing methods in terms of variable selection accuracy and regret.
High dimensional precision medicine from patient-derived xenografts
Dec 13, 2019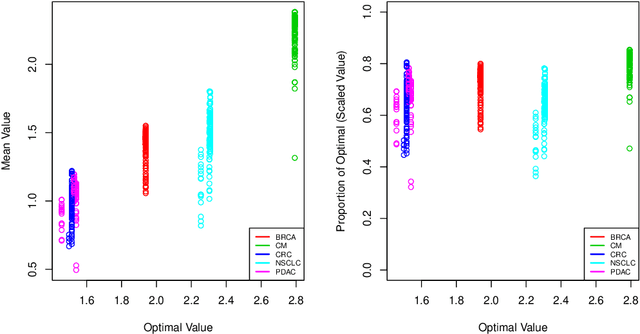

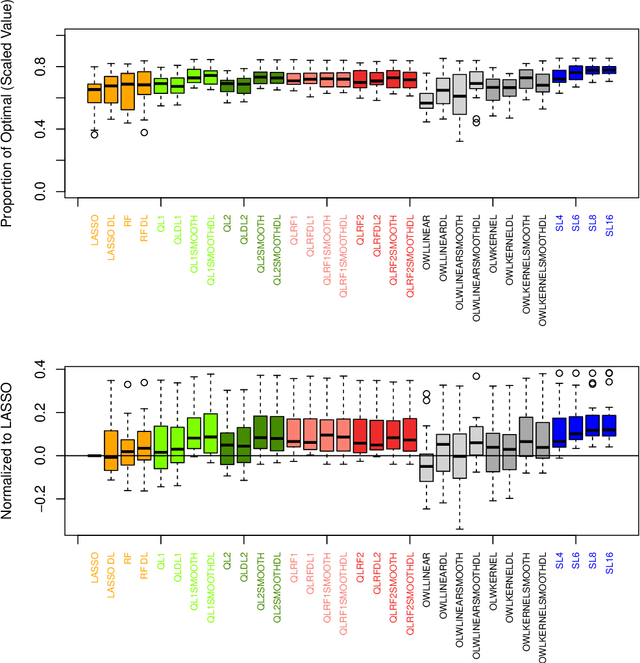
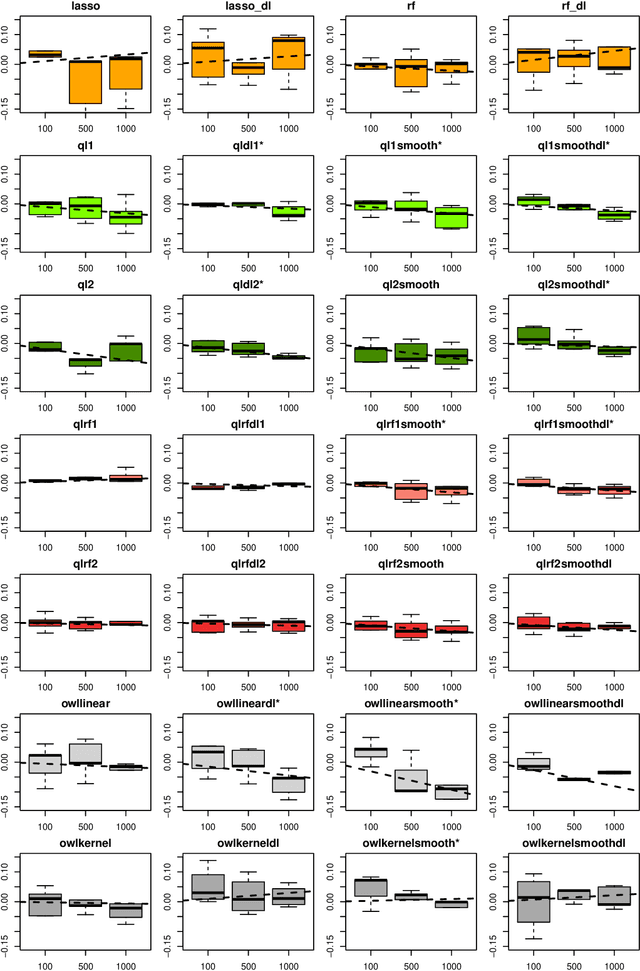
Abstract:The complexity of human cancer often results in significant heterogeneity in response to treatment. Precision medicine offers potential to improve patient outcomes by leveraging this heterogeneity. Individualized treatment rules (ITRs) formalize precision medicine as maps from the patient covariate space into the space of allowable treatments. The optimal ITR is that which maximizes the mean of a clinical outcome in a population of interest. Patient-derived xenograft (PDX) studies permit the evaluation of multiple treatments within a single tumor and thus are ideally suited for estimating optimal ITRs. PDX data are characterized by correlated outcomes, a high-dimensional feature space, and a large number of treatments. Existing methods for estimating optimal ITRs do not take advantage of the unique structure of PDX data or handle the associated challenges well. In this paper, we explore machine learning methods for estimating optimal ITRs from PDX data. We analyze data from a large PDX study to identify biomarkers that are informative for developing personalized treatment recommendations in multiple cancers. We estimate optimal ITRs using regression-based approaches such as Q-learning and direct search methods such as outcome weighted learning. Finally, we implement a superlearner approach to combine a set of estimated ITRs and show that the resulting ITR performs better than any of the input ITRs, mitigating uncertainty regarding user choice of any particular ITR estimation methodology. Our results indicate that PDX data are a valuable resource for developing individualized treatment strategies in oncology.
Global forensic geolocation with deep neural networks
May 28, 2019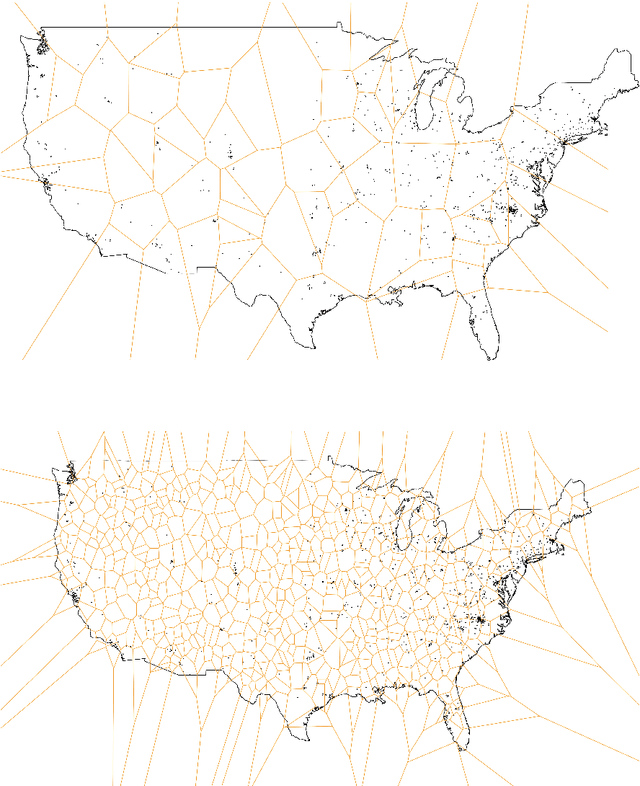
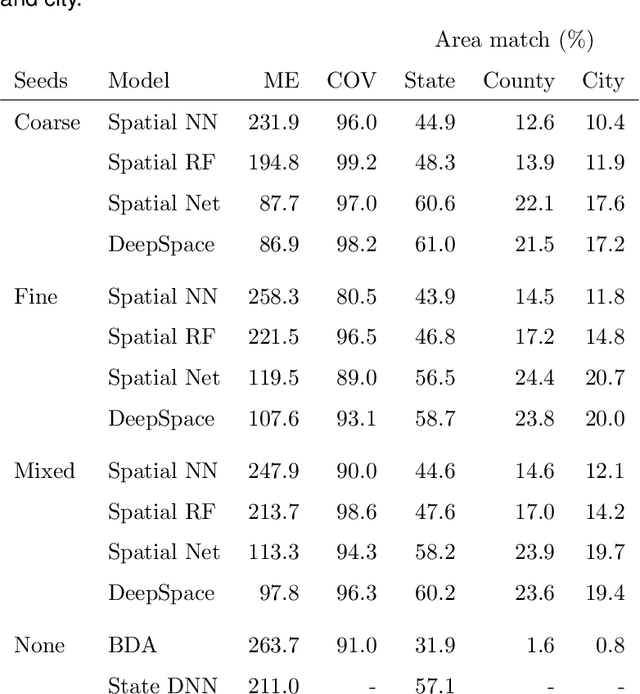
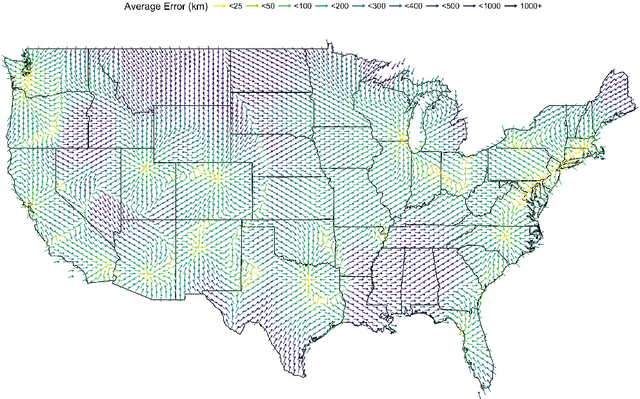
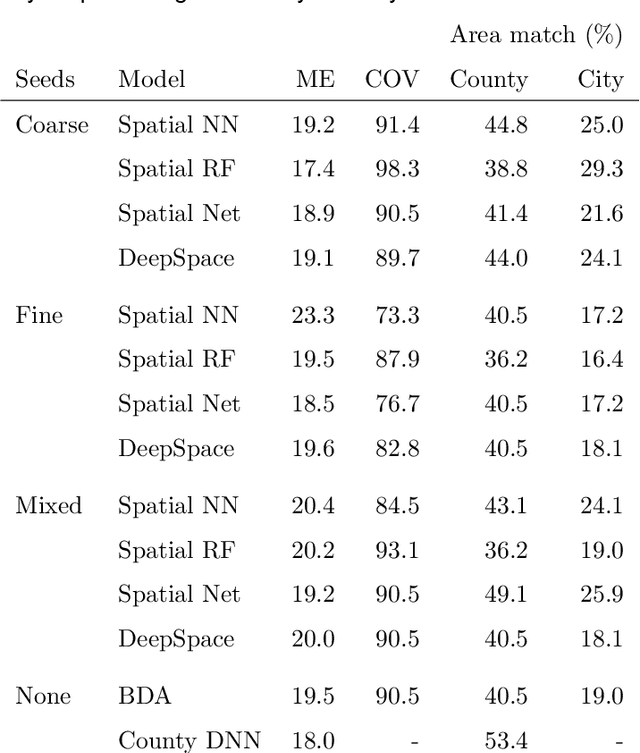
Abstract:An important problem in forensic analyses is identifying the provenance of materials at a crime scene, such as biological material on a piece of clothing. This procedure, known as geolocation, is conventionally guided by expert knowledge of the biological evidence and therefore tends to be application-specific, labor-intensive, and subjective. Purely data-driven methods have yet to be fully realized due in part to the lack of a sufficiently rich data source. However, high-throughput sequencing technologies are able to identify tens of thousands of microbial taxa using DNA recovered from a single swab collected from nearly any object or surface. We present a new algorithm for geolocation that aggregates over an ensemble of deep neural network classifiers trained on randomly-generated Voronoi partitions of a spatial domain. We apply the algorithm to fungi present in each of 1300 dust samples collected across the continental United States and then to a global dataset of dust samples from 28 countries. Our algorithm makes remarkably good point predictions with more than half of the geolocation errors under 100 kilometers for the continental analysis and nearly 90% classification accuracy of a sample's country of origin for the global analysis. We suggest that the effectiveness of this model sets the stage for a new, quantitative approach to forensic geolocation.
Thompson Sampling for Pursuit-Evasion Problems
Nov 11, 2018
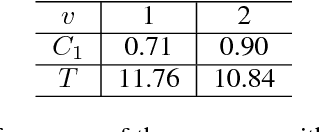


Abstract:Pursuit-evasion is a multi-agent sequential decision problem wherein a group of agents known as pursuers coordinate their traversal of a spatial domain to locate an agent trying to evade them. Pursuit evasion problems arise in a number of import application domains including defense and route planning. Learning to optimally coordinate pursuer behaviors so as to minimize time to capture of the evader is challenging because of a large action space and sparse noisy state information; consequently, previous approaches have relied primarily on heuristics. We propose a variant of Thompson Sampling for pursuit-evasion that allows for the application of existing model-based planning algorithms. This approach is general in that it allows for an arbitrary number of pursuers, a general spatial domain, and the integration of auxiliary information provided by informants. In a suite of simulation experiments, Thompson Sampling for pursuit evasion significantly reduces time-to-capture relative to competing algorithms.
Receiver Operating Characteristic Curves and Confidence Bands for Support Vector Machines
Jul 17, 2018
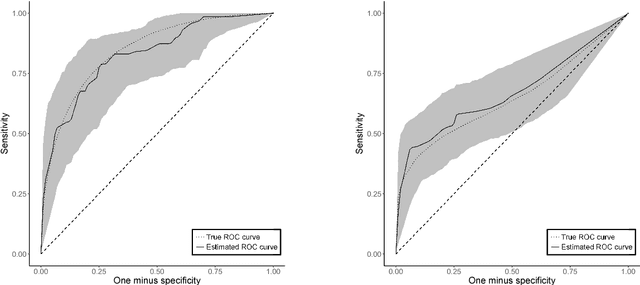
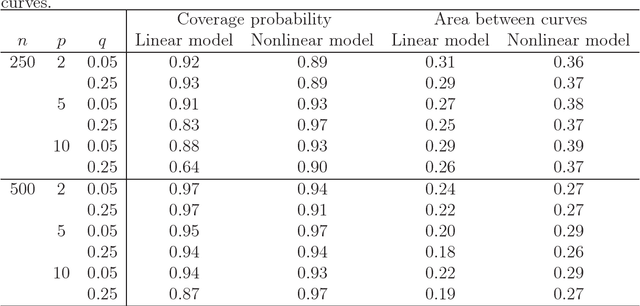
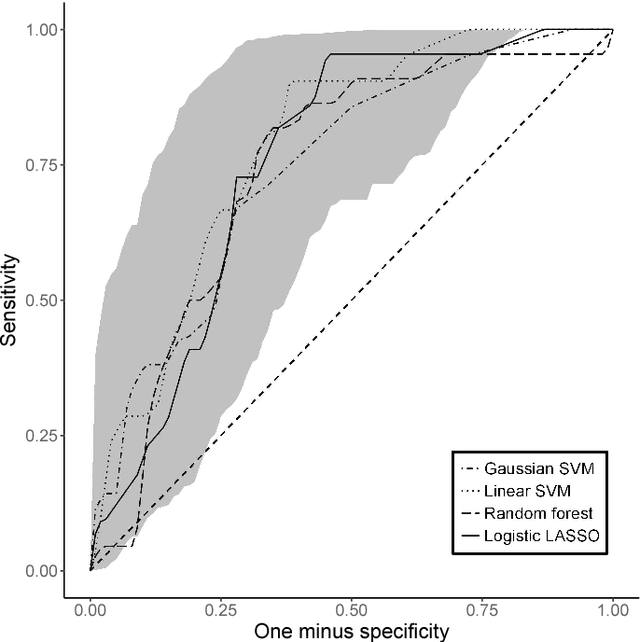
Abstract:Many problems that appear in biomedical decision making, such as diagnosing disease and predicting response to treatment, can be expressed as binary classification problems. The costs of false positives and false negatives vary across application domains and receiver operating characteristic (ROC) curves provide a visual representation of this trade-off. Nonparametric estimators for the ROC curve, such as a weighted support vector machine (SVM), are desirable because they are robust to model misspecification. While weighted SVMs have great potential for estimating ROC curves, their theoretical properties were heretofore underdeveloped. We propose a method for constructing confidence bands for the SVM ROC curve and provide the theoretical justification for the SVM ROC curve by showing that the risk function of the estimated decision rule is uniformly consistent across the weight parameter. We demonstrate the proposed confidence band method and the superior sensitivity and specificity of the weighted SVM compared to commonly used methods in diagnostic medicine using simulation studies. We present two illustrative examples: diagnosis of hepatitis C and a predictive model for treatment response in breast cancer.
Sufficient Markov Decision Processes with Alternating Deep Neural Networks
Mar 17, 2018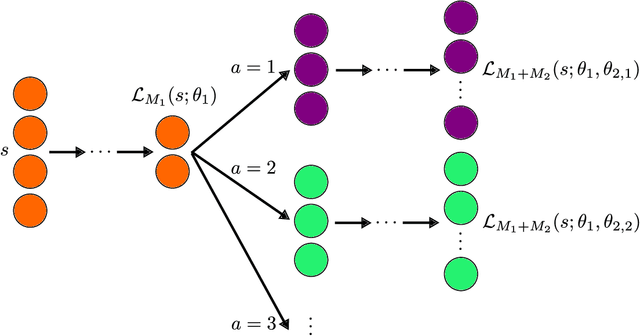
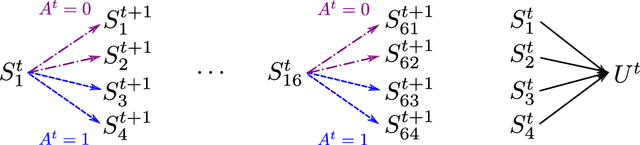
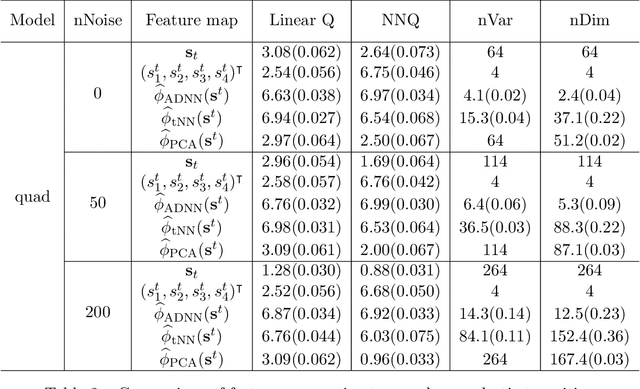
Abstract:Advances in mobile computing technologies have made it possible to monitor and apply data-driven interventions across complex systems in real time. Markov decision processes (MDPs) are the primary model for sequential decision problems with a large or indefinite time horizon. Choosing a representation of the underlying decision process that is both Markov and low-dimensional is non-trivial. We propose a method for constructing a low-dimensional representation of the original decision process for which: 1. the MDP model holds; 2. a decision strategy that maximizes mean utility when applied to the low-dimensional representation also maximizes mean utility when applied to the original process. We use a deep neural network to define a class of potential process representations and estimate the process of lowest dimension within this class. The method is illustrated using data from a mobile study on heavy drinking and smoking among college students.
Estimation and Optimization of Composite Outcomes
Feb 13, 2018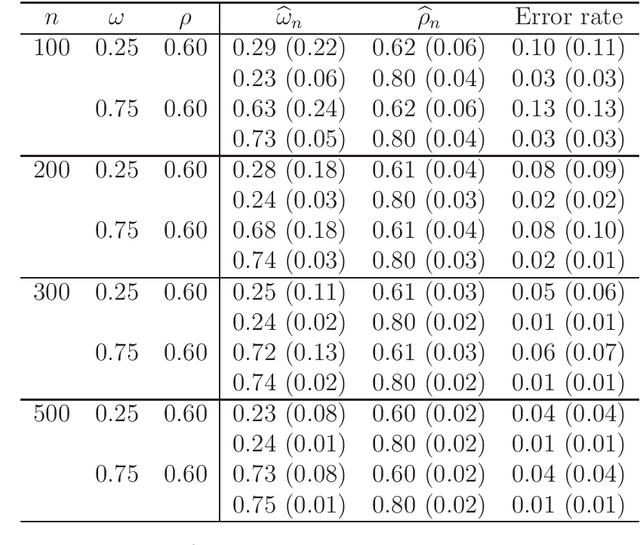
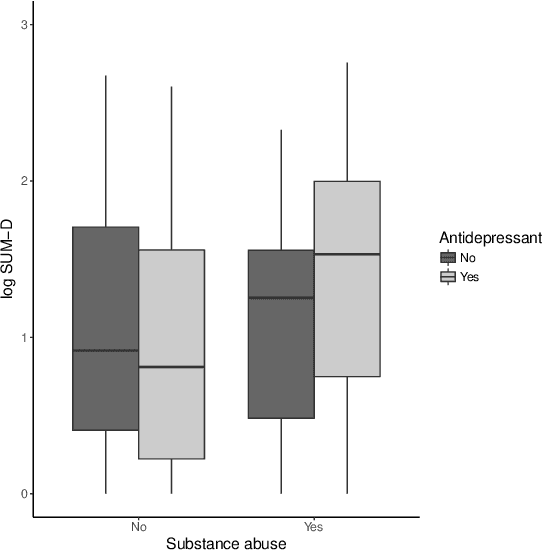
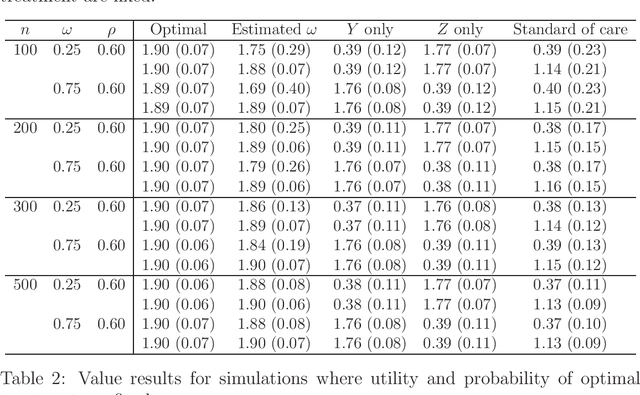
Abstract:There is tremendous interest in precision medicine as a means to improve patient outcomes by tailoring treatment to individual characteristics. An individualized treatment rule formalizes precision medicine as a map from patient information to a recommended treatment. A rule is defined to be optimal if it maximizes the mean of a scalar outcome in a population of interest, e.g., symptom reduction. However, clinical and intervention scientists often must balance multiple and possibly competing outcomes, e.g., symptom reduction and the risk of an adverse event. One approach to precision medicine in this setting is to elicit a composite outcome which balances all competing outcomes; unfortunately, eliciting a composite outcome directly from patients is difficult without a high-quality instrument and an expert-derived composite outcome may not account for heterogeneity in patient preferences. We consider estimation of composite outcomes using observational data under the assumption that clinicians are approximately (i.e., imperfectly) making decisions to maximize individual patient utility. Estimated composite outcomes are subsequently used to construct an estimator of an individualized treatment rule that maximizes the mean of patient-specific composite outcomes. Furthermore, the estimated composite outcomes and estimated optimal individualized treatment rule can provide new insights into patient preference heterogeneity, clinician behavior, and the value of precision medicine in a given domain. We derive inference procedures for the proposed estimators under mild conditions and demonstrate their finite sample performance through a suite of simulation experiments and an illustrative application to data from a study of bipolar depression.
Estimating Dynamic Treatment Regimes in Mobile Health Using V-learning
Oct 14, 2017
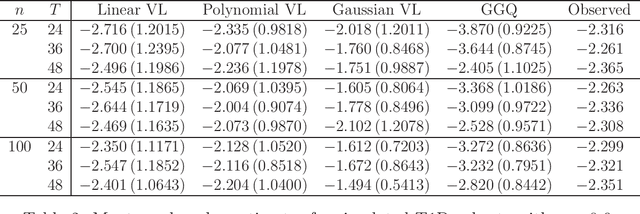


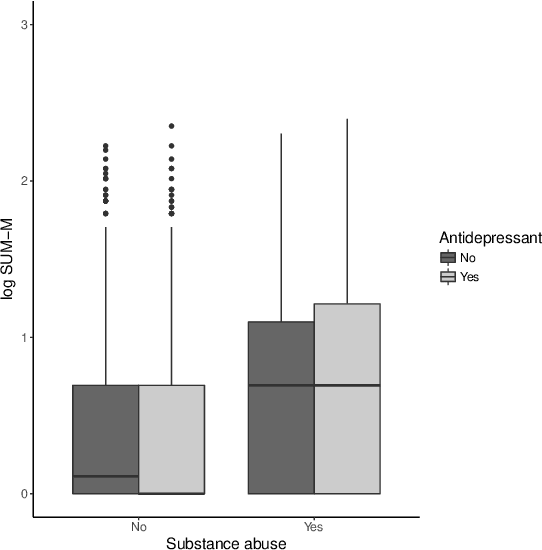
Abstract:The vision for precision medicine is to use individual patient characteristics to inform a personalized treatment plan that leads to the best healthcare possible for each patient. Mobile technologies have an important role to play in this vision as they offer a means to monitor a patient's health status in real-time and subsequently to deliver interventions if, when, and in the dose that they are needed. Dynamic treatment regimes formalize individualized treatment plans as sequences of decision rules, one per stage of clinical intervention, that map current patient information to a recommended treatment. However, existing methods for estimating optimal dynamic treatment regimes are designed for a small number of fixed decision points occurring on a coarse time-scale. We propose a new reinforcement learning method for estimating an optimal treatment regime that is applicable to data collected using mobile technologies in an outpatient setting. The proposed method accommodates an indefinite time horizon and minute-by-minute decision making that are common in mobile health applications. We show the proposed estimators are consistent and asymptotically normal under mild conditions. The proposed methods are applied to estimate an optimal dynamic treatment regime for controlling blood glucose levels in patients with type 1 diabetes.
$Q$- and $A$-Learning Methods for Estimating Optimal Dynamic Treatment Regimes
Feb 03, 2015
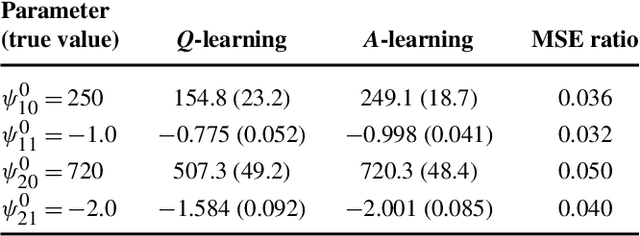

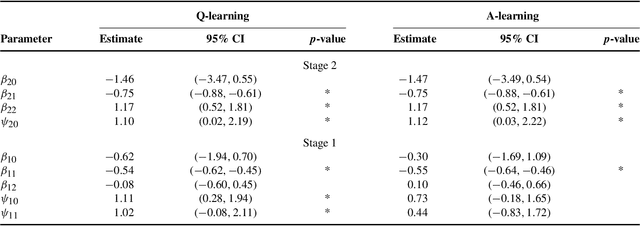
Abstract:In clinical practice, physicians make a series of treatment decisions over the course of a patient's disease based on his/her baseline and evolving characteristics. A dynamic treatment regime is a set of sequential decision rules that operationalizes this process. Each rule corresponds to a decision point and dictates the next treatment action based on the accrued information. Using existing data, a key goal is estimating the optimal regime, that, if followed by the patient population, would yield the most favorable outcome on average. Q- and A-learning are two main approaches for this purpose. We provide a detailed account of these methods, study their performance, and illustrate them using data from a depression study.
* Published in at http://dx.doi.org/10.1214/13-STS450 the Statistical Science (http://www.imstat.org/sts/) by the Institute of Mathematical Statistics (http://www.imstat.org)
Statistical Inference in Dynamic Treatment Regimes
Nov 26, 2013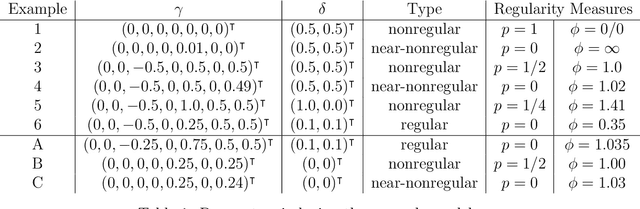
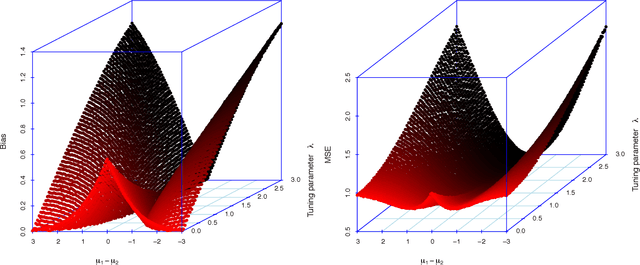
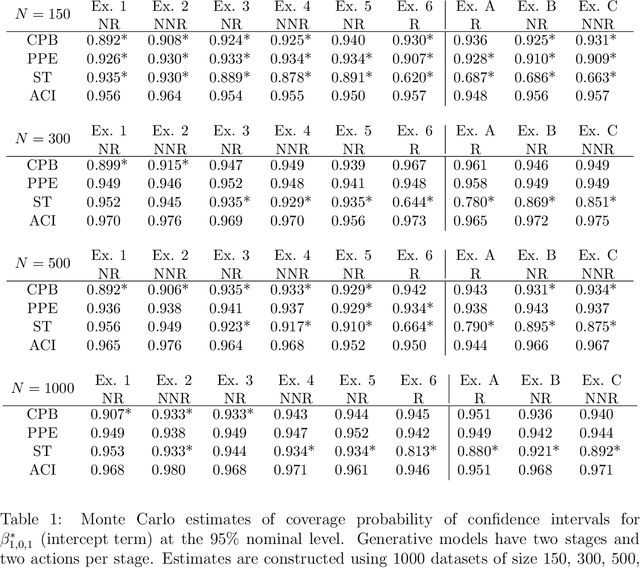
Abstract:Dynamic treatment regimes are of growing interest across the clinical sciences as these regimes provide one way to operationalize and thus inform sequential personalized clinical decision making. A dynamic treatment regime is a sequence of decision rules, with a decision rule per stage of clinical intervention; each decision rule maps up-to-date patient information to a recommended treatment. We briefly review a variety of approaches for using data to construct the decision rules. We then review an interesting challenge, that of nonregularity that often arises in this area. By nonregularity, we mean the parameters indexing the optimal dynamic treatment regime are nonsmooth functionals of the underlying generative distribution. A consequence is that no regular or asymptotically unbiased estimator of these parameters exists. Nonregularity arises in inference for parameters in the optimal dynamic treatment regime; we illustrate the effect of nonregularity on asymptotic bias and via sensitivity of asymptotic, limiting, distributions to local perturbations. We propose and evaluate a locally consistent Adaptive Confidence Interval (ACI) for the parameters of the optimal dynamic treatment regime. We use data from the Adaptive Interventions for Children with ADHD study as an illustrative example. We conclude by highlighting and discussing emerging theoretical problems in this area.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge