Sequential Knockoffs for Variable Selection in Reinforcement Learning
Paper and Code
Mar 24, 2023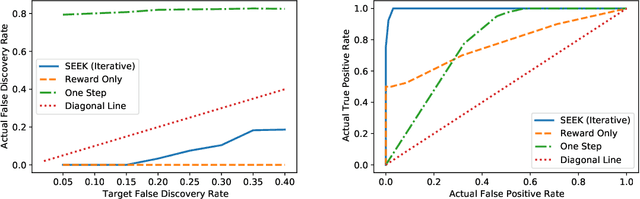


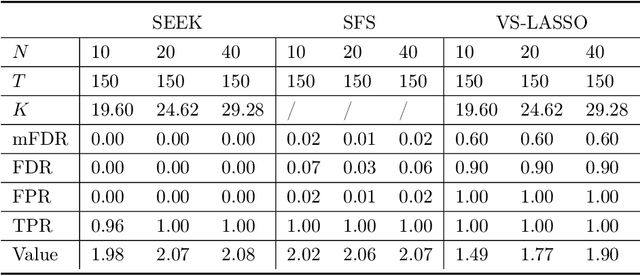
In real-world applications of reinforcement learning, it is often challenging to obtain a state representation that is parsimonious and satisfies the Markov property without prior knowledge. Consequently, it is common practice to construct a state which is larger than necessary, e.g., by concatenating measurements over contiguous time points. However, needlessly increasing the dimension of the state can slow learning and obfuscate the learned policy. We introduce the notion of a minimal sufficient state in a Markov decision process (MDP) as the smallest subvector of the original state under which the process remains an MDP and shares the same optimal policy as the original process. We propose a novel sequential knockoffs (SEEK) algorithm that estimates the minimal sufficient state in a system with high-dimensional complex nonlinear dynamics. In large samples, the proposed method controls the false discovery rate, and selects all sufficient variables with probability approaching one. As the method is agnostic to the reinforcement learning algorithm being applied, it benefits downstream tasks such as policy optimization. Empirical experiments verify theoretical results and show the proposed approach outperforms several competing methods in terms of variable selection accuracy and regret.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge