Weakly Supervised-Based Oversampling for High Imbalance and High Dimensionality Data Classification

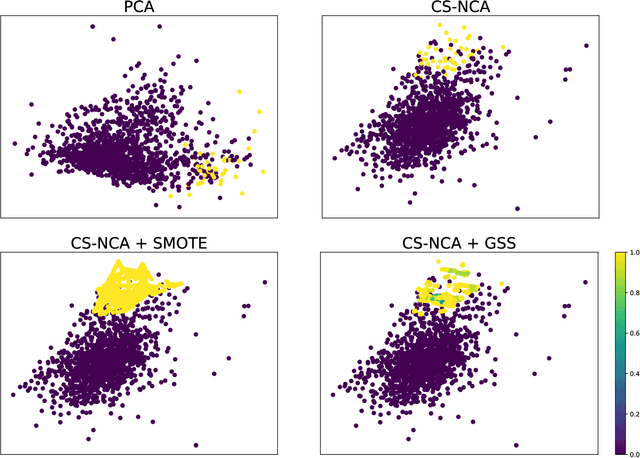
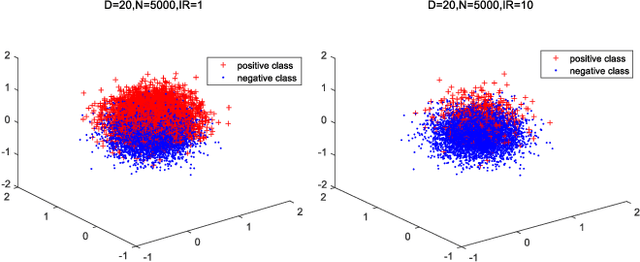
With the abundance of industrial datasets, imbalanced classification has become a common problem in several application domains. Oversampling is an effective method to solve imbalanced classification. One of the main challenges of the existing oversampling methods is to accurately label the new synthetic samples. Inaccurate labels of the synthetic samples would distort the distribution of the dataset and possibly worsen the classification performance. This paper introduces the idea of weakly supervised learning to handle the inaccurate labeling of synthetic samples caused by traditional oversampling methods. Graph semi-supervised SMOTE is developed to improve the credibility of the synthetic samples' labels. In addition, we propose cost-sensitive neighborhood components analysis for high dimensional datasets and bootstrap based ensemble framework for highly imbalanced datasets. The proposed method has achieved good classification performance on 8 synthetic datasets and 3 real-world datasets, especially for high imbalance and high dimensionality problems. The average performances and robustness are better than the benchmark methods.

Statistical Inference in Dynamic Treatment Regimes

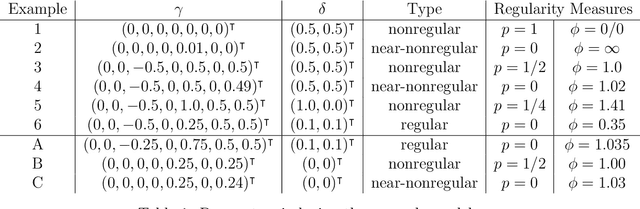
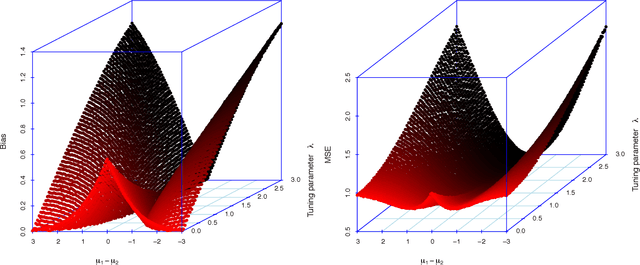
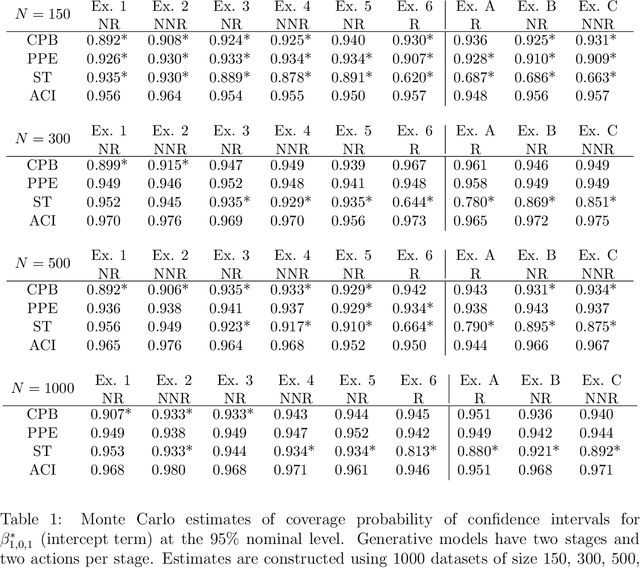
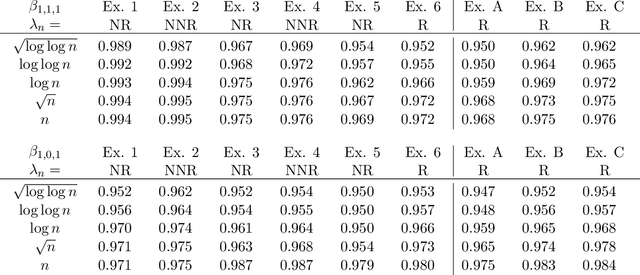
Dynamic treatment regimes are of growing interest across the clinical sciences as these regimes provide one way to operationalize and thus inform sequential personalized clinical decision making. A dynamic treatment regime is a sequence of decision rules, with a decision rule per stage of clinical intervention; each decision rule maps up-to-date patient information to a recommended treatment. We briefly review a variety of approaches for using data to construct the decision rules. We then review an interesting challenge, that of nonregularity that often arises in this area. By nonregularity, we mean the parameters indexing the optimal dynamic treatment regime are nonsmooth functionals of the underlying generative distribution. A consequence is that no regular or asymptotically unbiased estimator of these parameters exists. Nonregularity arises in inference for parameters in the optimal dynamic treatment regime; we illustrate the effect of nonregularity on asymptotic bias and via sensitivity of asymptotic, limiting, distributions to local perturbations. We propose and evaluate a locally consistent Adaptive Confidence Interval (ACI) for the parameters of the optimal dynamic treatment regime. We use data from the Adaptive Interventions for Children with ADHD study as an illustrative example. We conclude by highlighting and discussing emerging theoretical problems in this area.