Dynamic Classification of Latent Disease Progression with Auxiliary Surrogate Labels

Disease progression prediction based on patients' evolving health information is challenging when true disease states are unknown due to diagnostic capabilities or high costs. For example, the absence of gold-standard neurological diagnoses hinders distinguishing Alzheimer's disease (AD) from related conditions such as AD-related dementias (ADRDs), including Lewy body dementia (LBD). Combining temporally dependent surrogate labels and health markers may improve disease prediction. However, existing literature models informative surrogate labels and observed variables that reflect the underlying states using purely generative approaches, limiting the ability to predict future states. We propose integrating the conventional hidden Markov model as a generative model with a time-varying discriminative classification model to simultaneously handle potentially misspecified surrogate labels and incorporate important markers of disease progression. We develop an adaptive forward-backward algorithm with subjective labels for estimation, and utilize the modified posterior and Viterbi algorithms to predict the progression of future states or new patients based on objective markers only. Importantly, the adaptation eliminates the need to model the marginal distribution of longitudinal markers, a requirement in traditional algorithms. Asymptotic properties are established, and significant improvement with finite samples is demonstrated via simulation studies. Analysis of the neuropathological dataset of the National Alzheimer's Coordinating Center (NACC) shows much improved accuracy in distinguishing LBD from AD.

Fusing Individualized Treatment Rules Using Secondary Outcomes

An individualized treatment rule (ITR) is a decision rule that recommends treatments for patients based on their individual feature variables. In many practices, the ideal ITR for the primary outcome is also expected to cause minimal harm to other secondary outcomes. Therefore, our objective is to learn an ITR that not only maximizes the value function for the primary outcome, but also approximates the optimal rule for the secondary outcomes as closely as possible. To achieve this goal, we introduce a fusion penalty to encourage the ITRs based on different outcomes to yield similar recommendations. Two algorithms are proposed to estimate the ITR using surrogate loss functions. We prove that the agreement rate between the estimated ITR of the primary outcome and the optimal ITRs of the secondary outcomes converges to the true agreement rate faster than if the secondary outcomes are not taken into consideration. Furthermore, we derive the non-asymptotic properties of the value function and misclassification rate for the proposed method. Finally, simulation studies and a real data example are used to demonstrate the finite-sample performance of the proposed method.

Reinforcement Learning with Hidden Markov Models for Discovering Decision-Making Dynamics

Major depressive disorder (MDD) presents challenges in diagnosis and treatment due to its complex and heterogeneous nature. Emerging evidence indicates that reward processing abnormalities may serve as a behavioral marker for MDD. To measure reward processing, patients perform computer-based behavioral tasks that involve making choices or responding to stimulants that are associated with different outcomes. Reinforcement learning (RL) models are fitted to extract parameters that measure various aspects of reward processing to characterize how patients make decisions in behavioral tasks. Recent findings suggest the inadequacy of characterizing reward learning solely based on a single RL model; instead, there may be a switching of decision-making processes between multiple strategies. An important scientific question is how the dynamics of learning strategies in decision-making affect the reward learning ability of individuals with MDD. Motivated by the probabilistic reward task (PRT) within the EMBARC study, we propose a novel RL-HMM framework for analyzing reward-based decision-making. Our model accommodates learning strategy switching between two distinct approaches under a hidden Markov model (HMM): subjects making decisions based on the RL model or opting for random choices. We account for continuous RL state space and allow time-varying transition probabilities in the HMM. We introduce a computationally efficient EM algorithm for parameter estimation and employ a nonparametric bootstrap for inference. We apply our approach to the EMBARC study to show that MDD patients are less engaged in RL compared to the healthy controls, and engagement is associated with brain activities in the negative affect circuitry during an emotional conflict task.

Asymptotic Inference for Multi-Stage Stationary Treatment Policy with High Dimensional Features

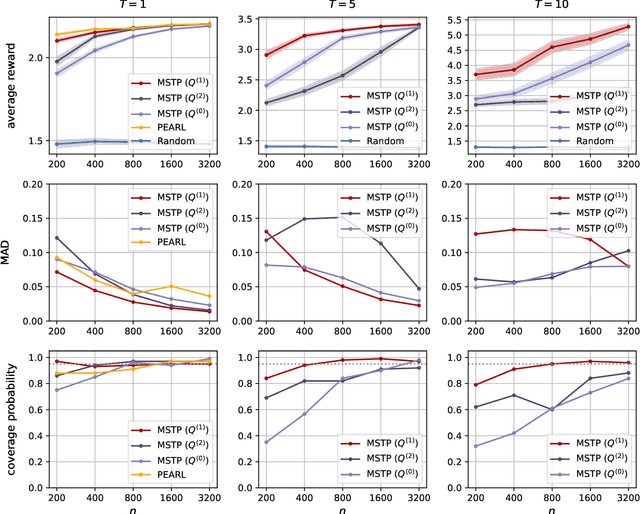
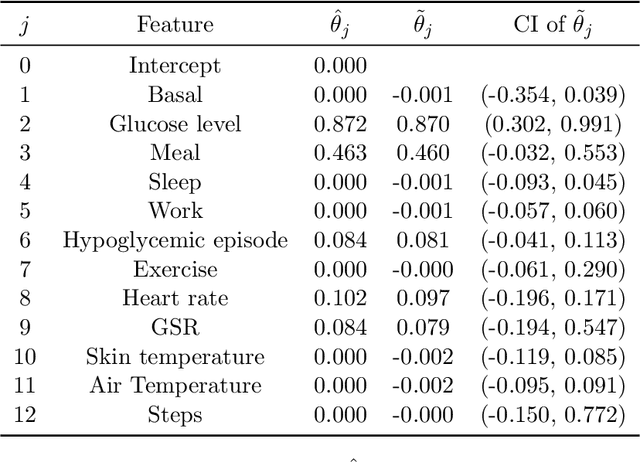
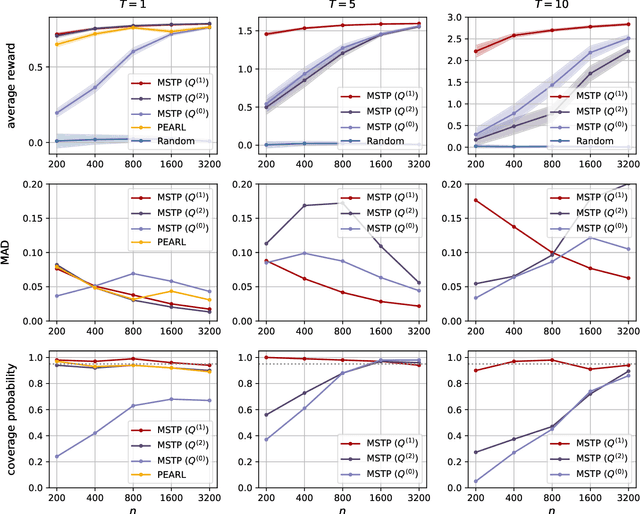
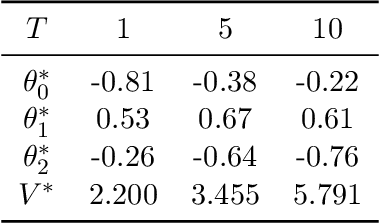
Dynamic treatment rules or policies are a sequence of decision functions over multiple stages that are tailored to individual features. One important class of treatment policies for practice, namely multi-stage stationary treatment policies, prescribe treatment assignment probabilities using the same decision function over stages, where the decision is based on the same set of features consisting of both baseline variables (e.g., demographics) and time-evolving variables (e.g., routinely collected disease biomarkers). Although there has been extensive literature to construct valid inference for the value function associated with the dynamic treatment policies, little work has been done for the policies themselves, especially in the presence of high dimensional feature variables. We aim to fill in the gap in this work. Specifically, we first estimate the multistage stationary treatment policy based on an augmented inverse probability weighted estimator for the value function to increase the asymptotic efficiency, and further apply a penalty to select important feature variables. We then construct one-step improvement of the policy parameter estimators. Theoretically, we show that the improved estimators are asymptotically normal, even if nuisance parameters are estimated at a slow convergence rate and the dimension of the feature variables increases exponentially with the sample size. Our numerical studies demonstrate that the proposed method has satisfactory performance in small samples, and that the performance can be improved with a choice of the augmentation term that approximates the rewards or minimizes the variance of the value function.

Exploratory Hidden Markov Factor Models for Longitudinal Mobile Health Data: Application to Adverse Posttraumatic Neuropsychiatric Sequelae

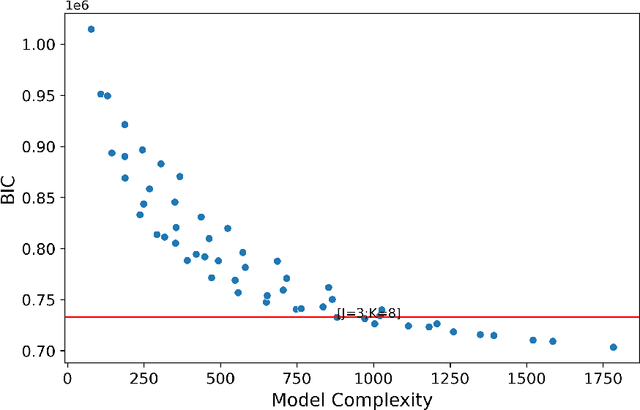
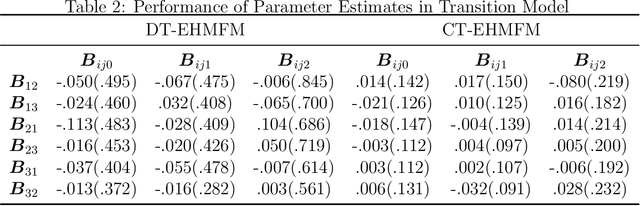
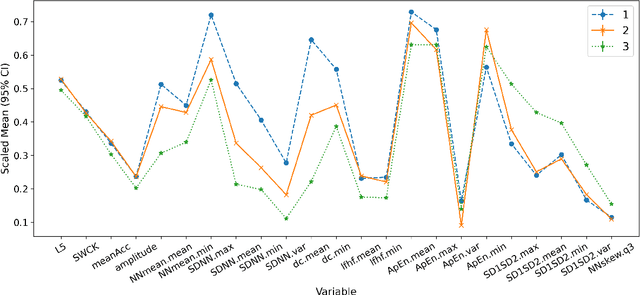
Adverse posttraumatic neuropsychiatric sequelae (APNS) are common among veterans and millions of Americans after traumatic events and cause tremendous burdens for trauma survivors and society. Many studies have been conducted to investigate the challenges in diagnosing and treating APNS symptoms. However, progress has been limited by the subjective nature of traditional measures. This study is motivated by the objective mobile device data collected from the Advancing Understanding of RecOvery afteR traumA (AURORA) study. We develop both discrete-time and continuous-time exploratory hidden Markov factor models to model the dynamic psychological conditions of individuals with either regular or irregular measurements. The proposed models extend the conventional hidden Markov models to allow high-dimensional data and feature-based nonhomogeneous transition probability between hidden psychological states. To find the maximum likelihood estimates, we develop a Stabilized Expectation-Maximization algorithm with Initialization Strategies (SEMIS). Simulation studies with synthetic data are carried out to assess the performance of parameter estimation and model selection. Finally, an application to the AURORA data is conducted, which captures the relationships between heart rate variability, activity, and APNS consistent with existing literature.

Representation Learning for Integrating Multi-domain Outcomes to Optimize Individualized Treatments

For mental disorders, patients' underlying mental states are non-observed latent constructs which have to be inferred from observed multi-domain measurements such as diagnostic symptoms and patient functioning scores. Additionally, substantial heterogeneity in the disease diagnosis between patients needs to be addressed for optimizing individualized treatment policy in order to achieve precision medicine. To address these challenges, we propose an integrated learning framework that can simultaneously learn patients' underlying mental states and recommend optimal treatments for each individual. This learning framework is based on the measurement theory in psychiatry for modeling multiple disease diagnostic measures as arising from the underlying causes (true mental states). It allows incorporation of the multivariate pre- and post-treatment outcomes as well as biological measures while preserving the invariant structure for representing patients' latent mental states. A multi-layer neural network is used to allow complex treatment effect heterogeneity. Optimal treatment policy can be inferred for future patients by comparing their potential mental states under different treatments given the observed multi-domain pre-treatment measurements. Experiments on simulated data and a real-world clinical trial data show that the learned treatment polices compare favorably to alternative methods on heterogeneous treatment effects, and have broad utilities which lead to better patient outcomes on multiple domains.

High dimensional precision medicine from patient-derived xenografts

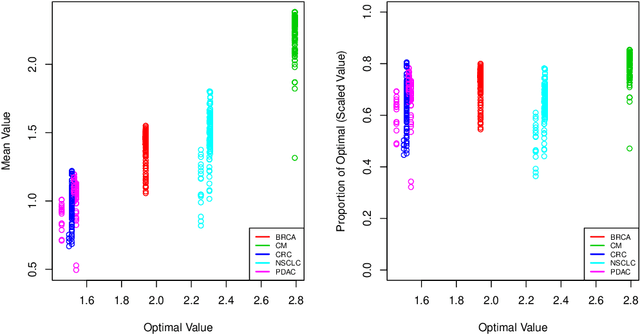
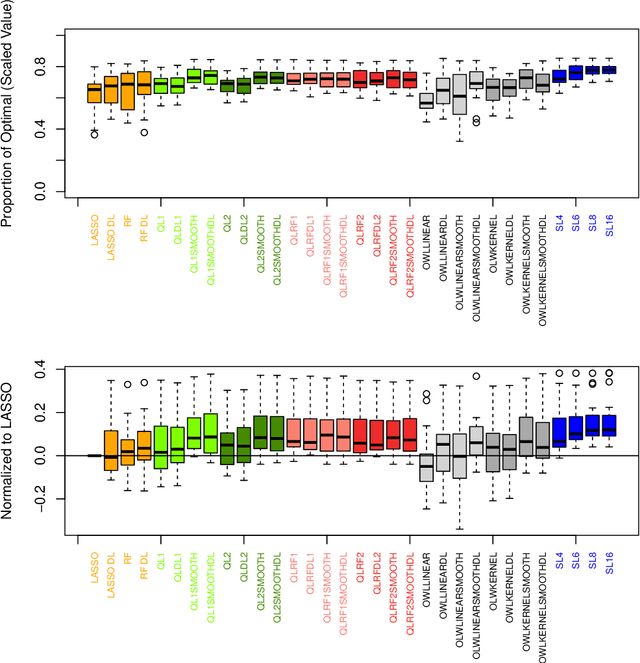
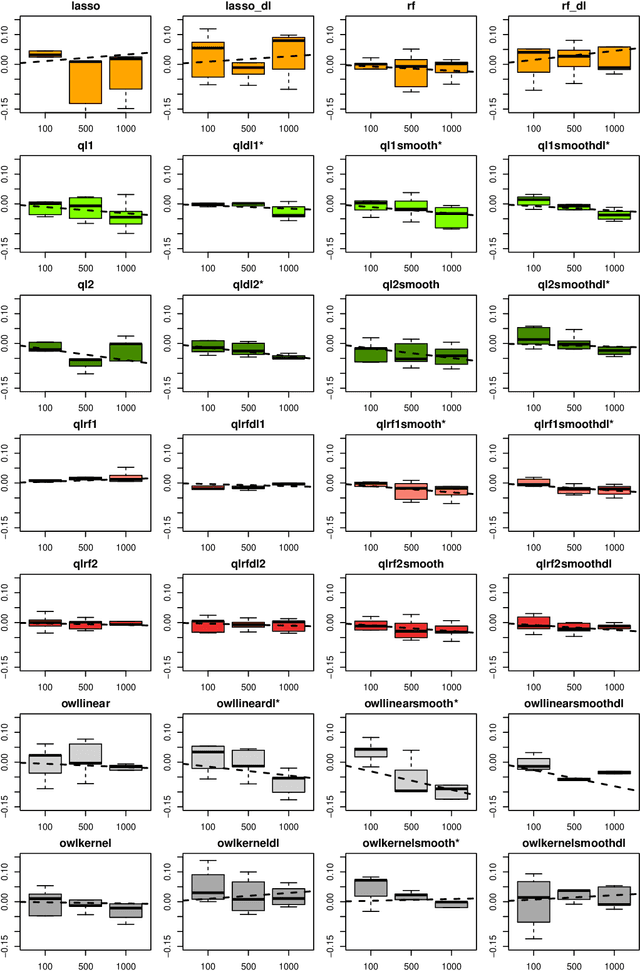
The complexity of human cancer often results in significant heterogeneity in response to treatment. Precision medicine offers potential to improve patient outcomes by leveraging this heterogeneity. Individualized treatment rules (ITRs) formalize precision medicine as maps from the patient covariate space into the space of allowable treatments. The optimal ITR is that which maximizes the mean of a clinical outcome in a population of interest. Patient-derived xenograft (PDX) studies permit the evaluation of multiple treatments within a single tumor and thus are ideally suited for estimating optimal ITRs. PDX data are characterized by correlated outcomes, a high-dimensional feature space, and a large number of treatments. Existing methods for estimating optimal ITRs do not take advantage of the unique structure of PDX data or handle the associated challenges well. In this paper, we explore machine learning methods for estimating optimal ITRs from PDX data. We analyze data from a large PDX study to identify biomarkers that are informative for developing personalized treatment recommendations in multiple cancers. We estimate optimal ITRs using regression-based approaches such as Q-learning and direct search methods such as outcome weighted learning. Finally, we implement a superlearner approach to combine a set of estimated ITRs and show that the resulting ITR performs better than any of the input ITRs, mitigating uncertainty regarding user choice of any particular ITR estimation methodology. Our results indicate that PDX data are a valuable resource for developing individualized treatment strategies in oncology.