Harnessing Causality in Reinforcement Learning With Bagged Decision Times

We consider reinforcement learning (RL) for a class of problems with bagged decision times. A bag contains a finite sequence of consecutive decision times. The transition dynamics are non-Markovian and non-stationary within a bag. Further, all actions within a bag jointly impact a single reward, observed at the end of the bag. Our goal is to construct an online RL algorithm to maximize the discounted sum of the bag-specific rewards. To handle non-Markovian transitions within a bag, we utilize an expert-provided causal directed acyclic graph (DAG). Based on the DAG, we construct the states as a dynamical Bayesian sufficient statistic of the observed history, which results in Markovian state transitions within and across bags. We then frame this problem as a periodic Markov decision process (MDP) that allows non-stationarity within a period. An online RL algorithm based on Bellman-equations for stationary MDPs is generalized to handle periodic MDPs. To justify the proposed RL algorithm, we show that our constructed state achieves the maximal optimal value function among all state constructions for a periodic MDP. Further we prove the Bellman optimality equations for periodic MDPs. We evaluate the proposed method on testbed variants, constructed with real data from a mobile health clinical trial.

Fusing Individualized Treatment Rules Using Secondary Outcomes

An individualized treatment rule (ITR) is a decision rule that recommends treatments for patients based on their individual feature variables. In many practices, the ideal ITR for the primary outcome is also expected to cause minimal harm to other secondary outcomes. Therefore, our objective is to learn an ITR that not only maximizes the value function for the primary outcome, but also approximates the optimal rule for the secondary outcomes as closely as possible. To achieve this goal, we introduce a fusion penalty to encourage the ITRs based on different outcomes to yield similar recommendations. Two algorithms are proposed to estimate the ITR using surrogate loss functions. We prove that the agreement rate between the estimated ITR of the primary outcome and the optimal ITRs of the secondary outcomes converges to the true agreement rate faster than if the secondary outcomes are not taken into consideration. Furthermore, we derive the non-asymptotic properties of the value function and misclassification rate for the proposed method. Finally, simulation studies and a real data example are used to demonstrate the finite-sample performance of the proposed method.

Asymptotic Inference for Multi-Stage Stationary Treatment Policy with High Dimensional Features

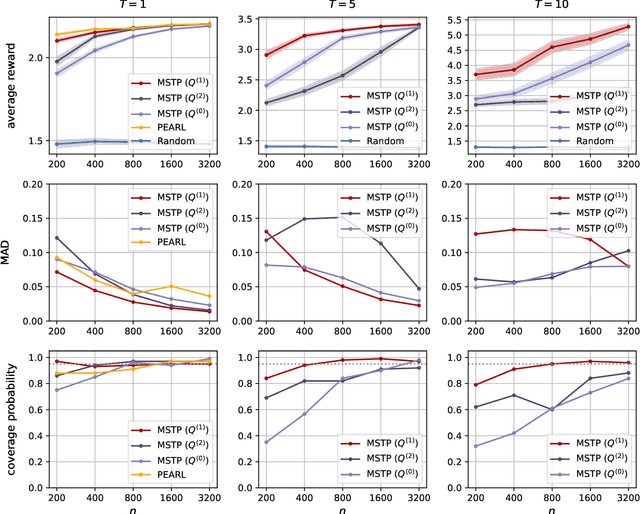
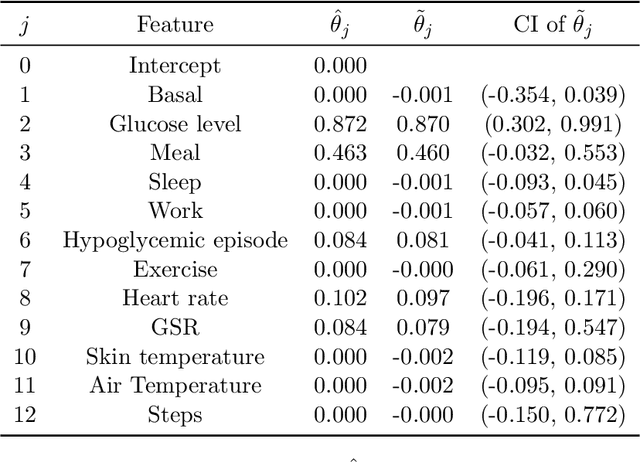
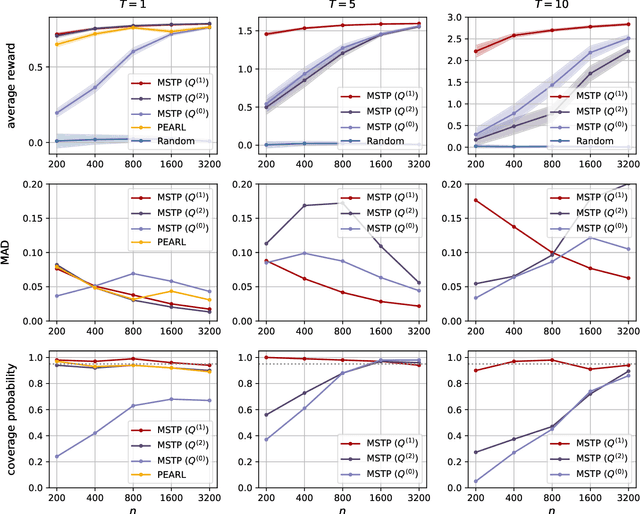
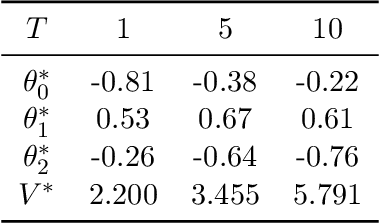
Dynamic treatment rules or policies are a sequence of decision functions over multiple stages that are tailored to individual features. One important class of treatment policies for practice, namely multi-stage stationary treatment policies, prescribe treatment assignment probabilities using the same decision function over stages, where the decision is based on the same set of features consisting of both baseline variables (e.g., demographics) and time-evolving variables (e.g., routinely collected disease biomarkers). Although there has been extensive literature to construct valid inference for the value function associated with the dynamic treatment policies, little work has been done for the policies themselves, especially in the presence of high dimensional feature variables. We aim to fill in the gap in this work. Specifically, we first estimate the multistage stationary treatment policy based on an augmented inverse probability weighted estimator for the value function to increase the asymptotic efficiency, and further apply a penalty to select important feature variables. We then construct one-step improvement of the policy parameter estimators. Theoretically, we show that the improved estimators are asymptotically normal, even if nuisance parameters are estimated at a slow convergence rate and the dimension of the feature variables increases exponentially with the sample size. Our numerical studies demonstrate that the proposed method has satisfactory performance in small samples, and that the performance can be improved with a choice of the augmentation term that approximates the rewards or minimizes the variance of the value function.