Daniel J. Luckett
Department of Biostatistics, University of North Carolina, Chapel Hill, North Carolina, U.S.A
High dimensional precision medicine from patient-derived xenografts
Dec 13, 2019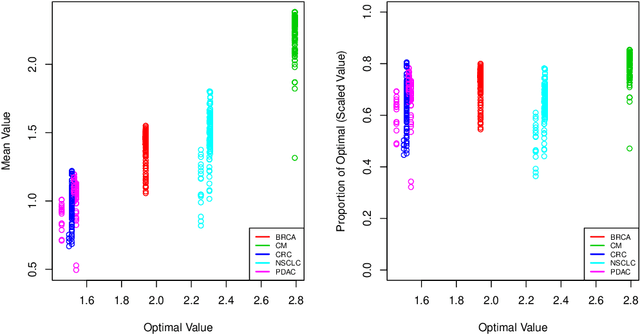

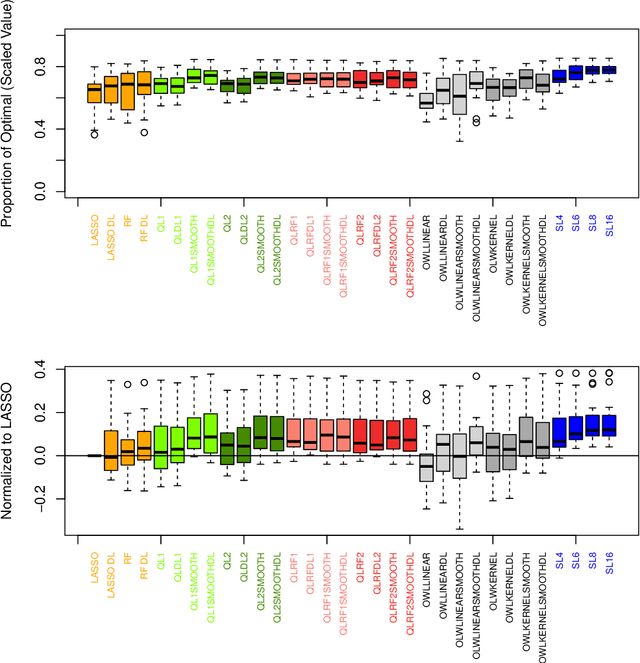
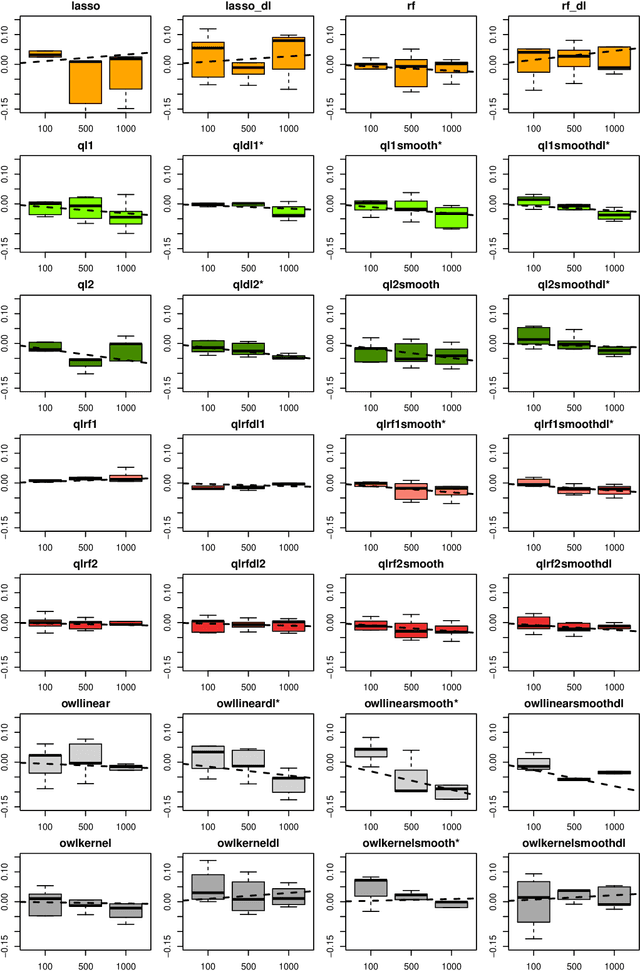
Abstract:The complexity of human cancer often results in significant heterogeneity in response to treatment. Precision medicine offers potential to improve patient outcomes by leveraging this heterogeneity. Individualized treatment rules (ITRs) formalize precision medicine as maps from the patient covariate space into the space of allowable treatments. The optimal ITR is that which maximizes the mean of a clinical outcome in a population of interest. Patient-derived xenograft (PDX) studies permit the evaluation of multiple treatments within a single tumor and thus are ideally suited for estimating optimal ITRs. PDX data are characterized by correlated outcomes, a high-dimensional feature space, and a large number of treatments. Existing methods for estimating optimal ITRs do not take advantage of the unique structure of PDX data or handle the associated challenges well. In this paper, we explore machine learning methods for estimating optimal ITRs from PDX data. We analyze data from a large PDX study to identify biomarkers that are informative for developing personalized treatment recommendations in multiple cancers. We estimate optimal ITRs using regression-based approaches such as Q-learning and direct search methods such as outcome weighted learning. Finally, we implement a superlearner approach to combine a set of estimated ITRs and show that the resulting ITR performs better than any of the input ITRs, mitigating uncertainty regarding user choice of any particular ITR estimation methodology. Our results indicate that PDX data are a valuable resource for developing individualized treatment strategies in oncology.
Estimating Individualized Treatment Regimes from Crossover Designs
Feb 05, 2019



Abstract:The field of precision medicine aims to tailor treatment based on patient-specific factors in a reproducible way. To this end, estimating an optimal individualized treatment regime (ITR) that recommends treatment decisions based on patient characteristics to maximize the mean of a pre-specified outcome is of particular interest. Several methods have been proposed for estimating an optimal ITR from clinical trial data in the parallel group setting where each subject is randomized to a single intervention. However, little work has been done in the area of estimating the optimal ITR from crossover study designs. Such designs naturally lend themselves to precision medicine, because they allow for observing the response to multiple treatments for each patient. In this paper, we introduce a method for estimating the optimal ITR using data from a 2x2 crossover study with or without carryover effects. The proposed method is similar to policy search methods such as outcome weighted learning; however, we take advantage of the crossover design by using the difference in responses under each treatment as the observed reward. We establish Fisher and global consistency, present numerical experiments, and analyze data from a feeding trial to demonstrate the improved performance of the proposed method compared to standard methods for a parallel study design.
Receiver Operating Characteristic Curves and Confidence Bands for Support Vector Machines
Jul 17, 2018
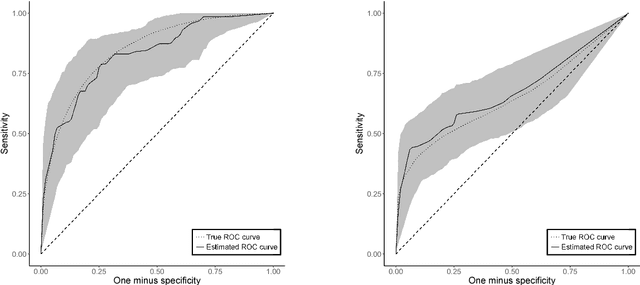
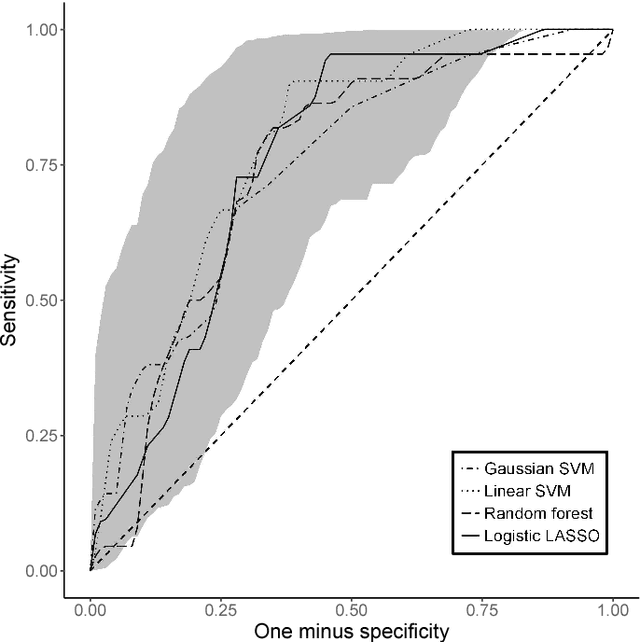
Abstract:Many problems that appear in biomedical decision making, such as diagnosing disease and predicting response to treatment, can be expressed as binary classification problems. The costs of false positives and false negatives vary across application domains and receiver operating characteristic (ROC) curves provide a visual representation of this trade-off. Nonparametric estimators for the ROC curve, such as a weighted support vector machine (SVM), are desirable because they are robust to model misspecification. While weighted SVMs have great potential for estimating ROC curves, their theoretical properties were heretofore underdeveloped. We propose a method for constructing confidence bands for the SVM ROC curve and provide the theoretical justification for the SVM ROC curve by showing that the risk function of the estimated decision rule is uniformly consistent across the weight parameter. We demonstrate the proposed confidence band method and the superior sensitivity and specificity of the weighted SVM compared to commonly used methods in diagnostic medicine using simulation studies. We present two illustrative examples: diagnosis of hepatitis C and a predictive model for treatment response in breast cancer.
Estimation and Optimization of Composite Outcomes
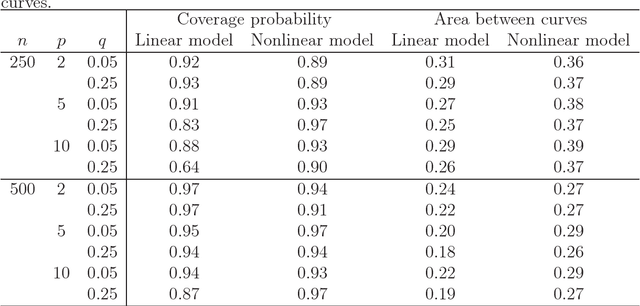
Feb 13, 2018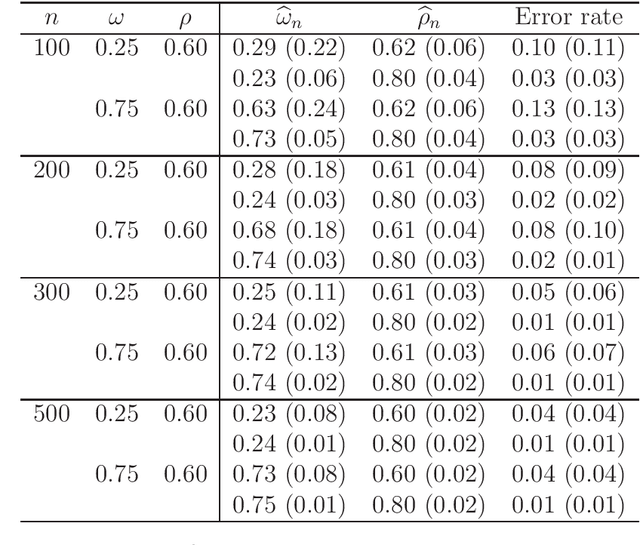
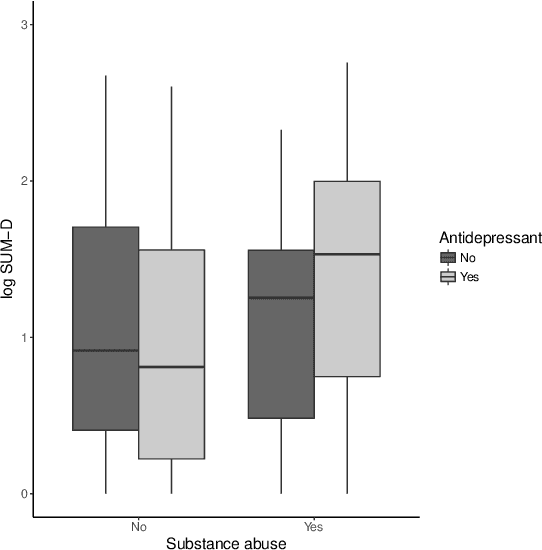
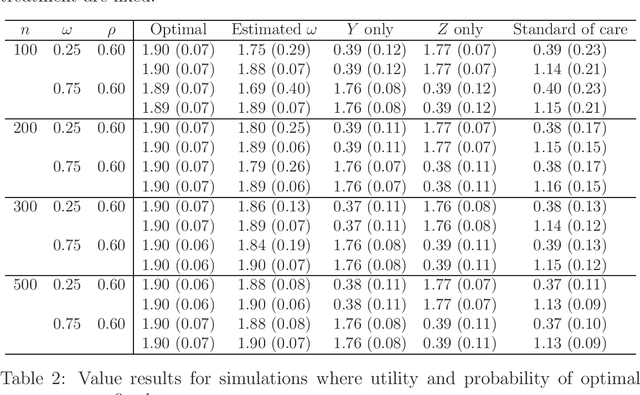
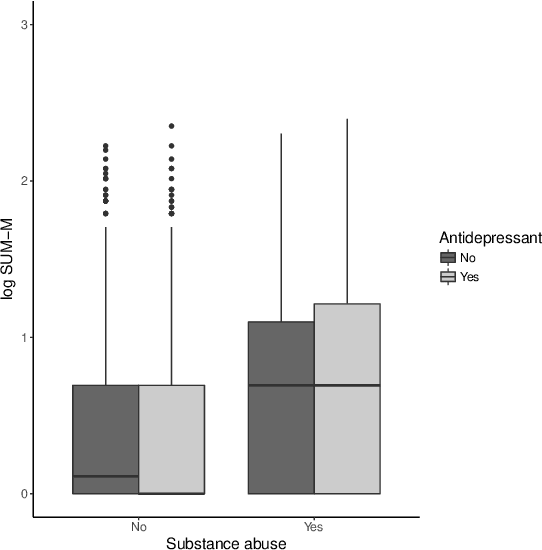
Abstract:There is tremendous interest in precision medicine as a means to improve patient outcomes by tailoring treatment to individual characteristics. An individualized treatment rule formalizes precision medicine as a map from patient information to a recommended treatment. A rule is defined to be optimal if it maximizes the mean of a scalar outcome in a population of interest, e.g., symptom reduction. However, clinical and intervention scientists often must balance multiple and possibly competing outcomes, e.g., symptom reduction and the risk of an adverse event. One approach to precision medicine in this setting is to elicit a composite outcome which balances all competing outcomes; unfortunately, eliciting a composite outcome directly from patients is difficult without a high-quality instrument and an expert-derived composite outcome may not account for heterogeneity in patient preferences. We consider estimation of composite outcomes using observational data under the assumption that clinicians are approximately (i.e., imperfectly) making decisions to maximize individual patient utility. Estimated composite outcomes are subsequently used to construct an estimator of an individualized treatment rule that maximizes the mean of patient-specific composite outcomes. Furthermore, the estimated composite outcomes and estimated optimal individualized treatment rule can provide new insights into patient preference heterogeneity, clinician behavior, and the value of precision medicine in a given domain. We derive inference procedures for the proposed estimators under mild conditions and demonstrate their finite sample performance through a suite of simulation experiments and an illustrative application to data from a study of bipolar depression.
Estimating Dynamic Treatment Regimes in Mobile Health Using V-learning
Oct 14, 2017
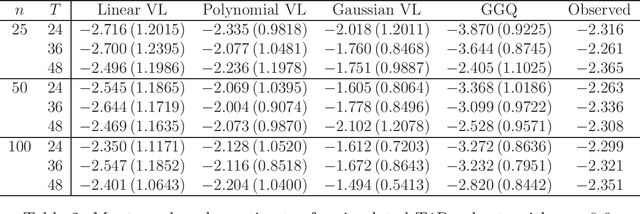


Abstract:The vision for precision medicine is to use individual patient characteristics to inform a personalized treatment plan that leads to the best healthcare possible for each patient. Mobile technologies have an important role to play in this vision as they offer a means to monitor a patient's health status in real-time and subsequently to deliver interventions if, when, and in the dose that they are needed. Dynamic treatment regimes formalize individualized treatment plans as sequences of decision rules, one per stage of clinical intervention, that map current patient information to a recommended treatment. However, existing methods for estimating optimal dynamic treatment regimes are designed for a small number of fixed decision points occurring on a coarse time-scale. We propose a new reinforcement learning method for estimating an optimal treatment regime that is applicable to data collected using mobile technologies in an outpatient setting. The proposed method accommodates an indefinite time horizon and minute-by-minute decision making that are common in mobile health applications. We show the proposed estimators are consistent and asymptotically normal under mild conditions. The proposed methods are applied to estimate an optimal dynamic treatment regime for controlling blood glucose levels in patients with type 1 diabetes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge