Multi-Task Combinatorial Bandits for Budget Allocation

Today's top advertisers typically manage hundreds of campaigns simultaneously and consistently launch new ones throughout the year. A crucial challenge for marketing managers is determining the optimal allocation of limited budgets across various ad lines in each campaign to maximize cumulative returns, especially given the huge uncertainty in return outcomes. In this paper, we propose to formulate budget allocation as a multi-task combinatorial bandit problem and introduce a novel online budget allocation system. The proposed system: i) integrates a Bayesian hierarchical model to intelligently utilize the metadata of campaigns and ad lines and budget size, ensuring efficient information sharing; ii) provides the flexibility to incorporate diverse modeling techniques such as Linear Regression, Gaussian Processes, and Neural Networks, catering to diverse environmental complexities; and iii) employs the Thompson sampling (TS) technique to strike a balance between exploration and exploitation. Through offline evaluation and online experiments, our system demonstrates robustness and adaptability, effectively maximizing the overall cumulative returns. A Python implementation of the proposed procedure is available at https://anonymous.4open.science/r/MCMAB.

Large Language Model for Causal Decision Making

Large Language Models (LLMs) have shown their success in language understanding and reasoning on general topics. However, their capability to inference based on user-specified structured data and knowledge in corpus-rare concepts like causal decision-making is still limited. In this work, we explore the possibility of fine-tuning an open-sourced LLM into LLM4Causal, which can identify the causal task, execute a corresponding function, and interpret its numerical results based on users' queries and the provided dataset. Meanwhile, we propose a data generation process for more controllable GPT prompting and present two instruction-tuning datasets: (1) Causal-Retrieval-Bench for causal problem identification and input parameter extraction for causal function calling and (2) Causal-Interpret-Bench for in-context causal interpretation. With three case studies, we showed that LLM4Causal can deliver end-to-end solutions for causal problems and provide easy-to-understand answers. Numerical studies also reveal that it has a remarkable ability to identify the correct causal task given a query.

A Reinforcement Learning Framework for Dynamic Mediation Analysis

Mediation analysis learns the causal effect transmitted via mediator variables between treatments and outcomes and receives increasing attention in various scientific domains to elucidate causal relations. Most existing works focus on point-exposure studies where each subject only receives one treatment at a single time point. However, there are a number of applications (e.g., mobile health) where the treatments are sequentially assigned over time and the dynamic mediation effects are of primary interest. Proposing a reinforcement learning (RL) framework, we are the first to evaluate dynamic mediation effects in settings with infinite horizons. We decompose the average treatment effect into an immediate direct effect, an immediate mediation effect, a delayed direct effect, and a delayed mediation effect. Upon the identification of each effect component, we further develop robust and semi-parametrically efficient estimators under the RL framework to infer these causal effects. The superior performance of the proposed method is demonstrated through extensive numerical studies, theoretical results, and an analysis of a mobile health dataset.

Towards Scalable and Robust Structured Bandits: A Meta-Learning Framework

Online learning in large-scale structured bandits is known to be challenging due to the curse of dimensionality. In this paper, we propose a unified meta-learning framework for a general class of structured bandit problems where the parameter space can be factorized to item-level. The novel bandit algorithm is general to be applied to many popular problems,scalable to the huge parameter and action spaces, and robust to the specification of the generalization model. At the core of this framework is a Bayesian hierarchical model that allows information sharing among items via their features, upon which we design a meta Thompson sampling algorithm. Three representative examples are discussed thoroughly. Both theoretical analysis and numerical results support the usefulness of the proposed method.

Exploratory Hidden Markov Factor Models for Longitudinal Mobile Health Data: Application to Adverse Posttraumatic Neuropsychiatric Sequelae

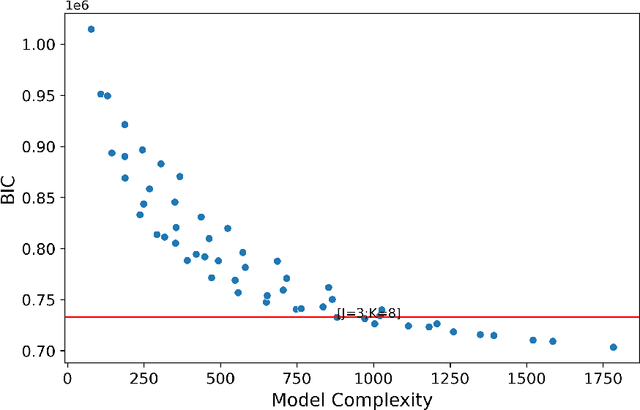
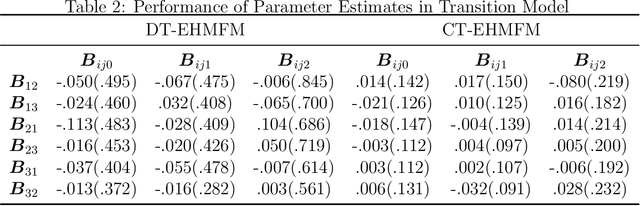
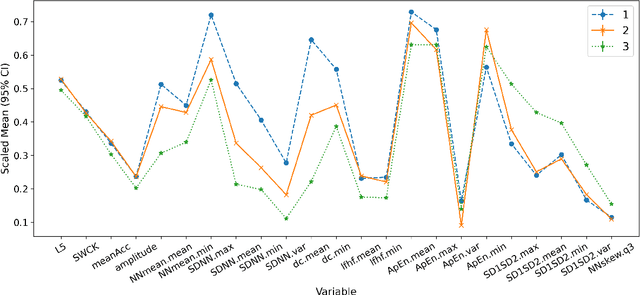
Adverse posttraumatic neuropsychiatric sequelae (APNS) are common among veterans and millions of Americans after traumatic events and cause tremendous burdens for trauma survivors and society. Many studies have been conducted to investigate the challenges in diagnosing and treating APNS symptoms. However, progress has been limited by the subjective nature of traditional measures. This study is motivated by the objective mobile device data collected from the Advancing Understanding of RecOvery afteR traumA (AURORA) study. We develop both discrete-time and continuous-time exploratory hidden Markov factor models to model the dynamic psychological conditions of individuals with either regular or irregular measurements. The proposed models extend the conventional hidden Markov models to allow high-dimensional data and feature-based nonhomogeneous transition probability between hidden psychological states. To find the maximum likelihood estimates, we develop a Stabilized Expectation-Maximization algorithm with Initialization Strategies (SEMIS). Simulation studies with synthetic data are carried out to assess the performance of parameter estimation and model selection. Finally, an application to the AURORA data is conducted, which captures the relationships between heart rate variability, activity, and APNS consistent with existing literature.

Metadata-based Multi-Task Bandits with Bayesian Hierarchical Models

How to explore efficiently is a central problem in multi-armed bandits. In this paper, we introduce the metadata-based multi-task bandit problem, where the agent needs to solve a large number of related multi-armed bandit tasks and can leverage some task-specific features (i.e., metadata) to share knowledge across tasks. As a general framework, we propose to capture task relations through the lens of Bayesian hierarchical models, upon which a Thompson sampling algorithm is designed to efficiently learn task relations, share information, and minimize the cumulative regrets. Two concrete examples for Gaussian bandits and Bernoulli bandits are carefully analyzed. The Bayes regret for Gaussian bandits clearly demonstrates the benefits of information sharing with our algorithm. The proposed method is further supported by extensive experiments.