Towards black-box parameter estimation

Deep learning algorithms have recently shown to be a successful tool in estimating parameters of statistical models for which simulation is easy, but likelihood computation is challenging. But the success of these approaches depends on simulating parameters that sufficiently reproduce the observed data, and, at present, there is a lack of efficient methods to produce these simulations. We develop new black-box procedures to estimate parameters of statistical models based only on weak parameter structure assumptions. For well-structured likelihoods with frequent occurrences, such as in time series, this is achieved by pre-training a deep neural network on an extensive simulated database that covers a wide range of data sizes. For other types of complex dependencies, an iterative algorithm guides simulations to the correct parameter region in multiple rounds. These approaches can successfully estimate and quantify the uncertainty of parameters from non-Gaussian models with complex spatial and temporal dependencies. The success of our methods is a first step towards a fully flexible automatic black-box estimation framework.

Correcting the Laplace Method with Variational Bayes

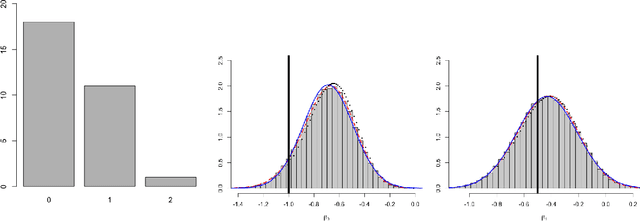
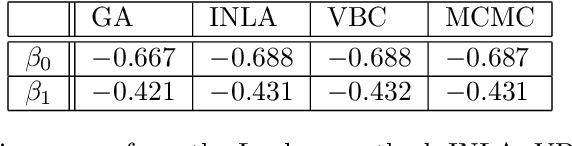
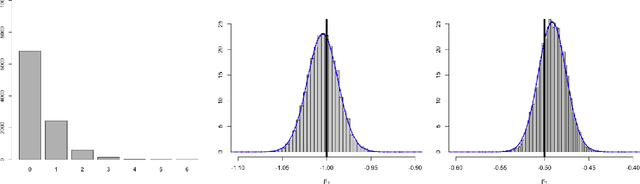
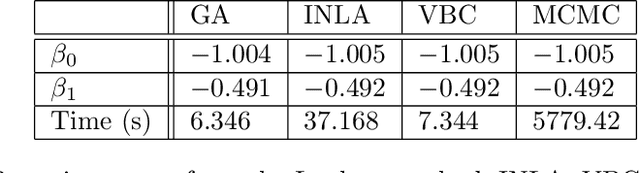
Approximate inference methods like the Laplace method, Laplace approximations and variational methods, amongst others, are popular methods when exact inference is not feasible due to the complexity of the model or the abundance of data. In this paper we propose a hybrid approximate method namely Low-Rank Variational Bayes correction (VBC), that uses the Laplace method and subsequently a Variational Bayes correction to the posterior mean. The cost is essentially that of the Laplace method which ensures scalability of the method. We illustrate the method and its advantages with simulated and real data, on small and large scale.