Deep Learning of Multivariate Extremes via a Geometric Representation

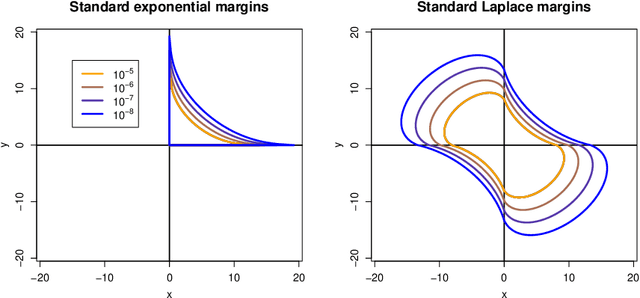
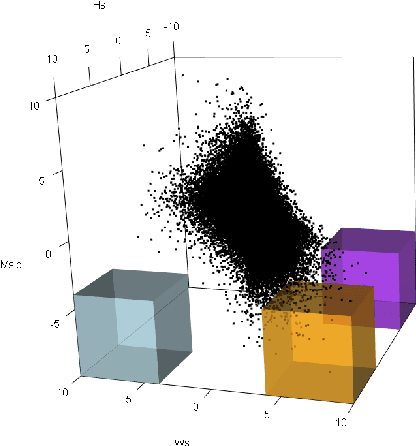
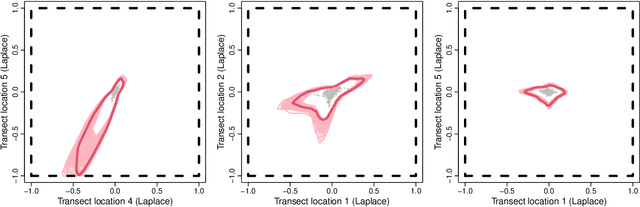
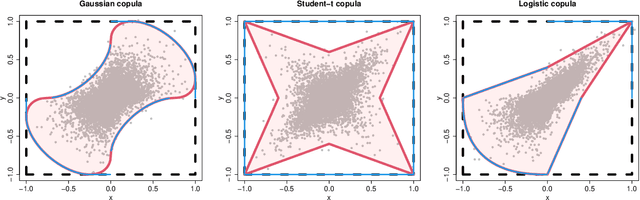
The study of geometric extremes, where extremal dependence properties are inferred from the deterministic limiting shapes of scaled sample clouds, provides an exciting approach to modelling the extremes of multivariate data. These shapes, termed limit sets, link together several popular extremal dependence modelling frameworks. Although the geometric approach is becoming an increasingly popular modelling tool, current inference techniques are limited to a low dimensional setting (d < 4), and generally require rigid modelling assumptions. In this work, we propose a range of novel theoretical results to aid with the implementation of the geometric extremes framework and introduce the first approach to modelling limit sets using deep learning. By leveraging neural networks, we construct asymptotically-justified yet flexible semi-parametric models for extremal dependence of high-dimensional data. We showcase the efficacy of our deep approach by modelling the complex extremal dependencies between meteorological and oceanographic variables in the North Sea off the coast of the UK.