FedBC: Calibrating Global and Local Models via Federated Learning Beyond Consensus
Paper and Code
Jun 26, 2022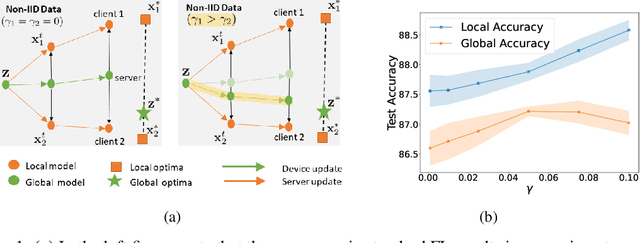
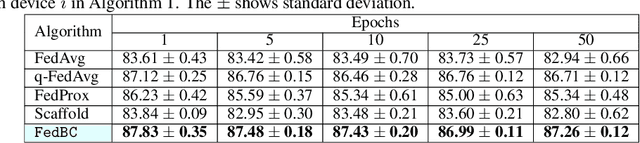
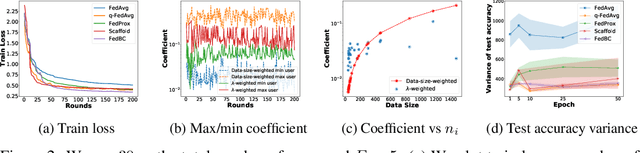
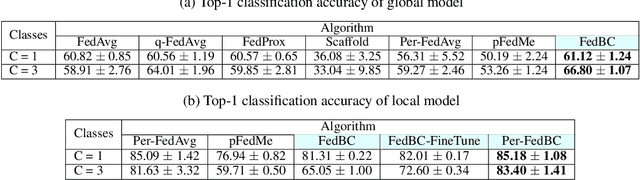
In federated learning (FL), the objective of collaboratively learning a global model through aggregation of model updates across devices tends to oppose the goal of personalization via local information. In this work, we calibrate this tradeoff in a quantitative manner through a multi-criterion optimization-based framework, which we cast as a constrained program: the objective for a device is its local objective, which it seeks to minimize while satisfying nonlinear constraints that quantify the proximity between the local and the global model. By considering the Lagrangian relaxation of this problem, we develop an algorithm that allows each node to minimize its local component of Lagrangian through queries to a first-order gradient oracle. Then, the server executes Lagrange multiplier ascent steps followed by a Lagrange multiplier-weighted averaging step. We call this instantiation of the primal-dual method Federated Learning Beyond Consensus ($\texttt{FedBC}$). Theoretically, we establish that $\texttt{FedBC}$ converges to a first-order stationary point at rates that matches the state of the art, up to an additional error term that depends on the tolerance parameter that arises due to the proximity constraints. Overall, the analysis is a novel characterization of primal-dual methods applied to non-convex saddle point problems with nonlinear constraints. Finally, we demonstrate that $\texttt{FedBC}$ balances the global and local model test accuracy metrics across a suite of datasets (Synthetic, MNIST, CIFAR-10, Shakespeare), achieving competitive performance with the state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge