Don't Be So Positive: Negative Step Sizes in Second-Order Methods

The value of second-order methods lies in the use of curvature information. Yet, this information is costly to extract and once obtained, valuable negative curvature information is often discarded so that the method is globally convergent. This limits the effectiveness of second-order methods in modern machine learning. In this paper, we show that second-order and second-order-like methods are promising optimizers for neural networks provided that we add one ingredient: negative step sizes. We show that under very general conditions, methods that produce ascent directions are globally convergent when combined with a Wolfe line search that allows both positive and negative step sizes. We experimentally demonstrate that using negative step sizes is often more effective than common Hessian modification methods.

Why Line Search when you can Plane Search? SO-Friendly Neural Networks allow Per-Iteration Optimization of Learning and Momentum Rates for Every Layer

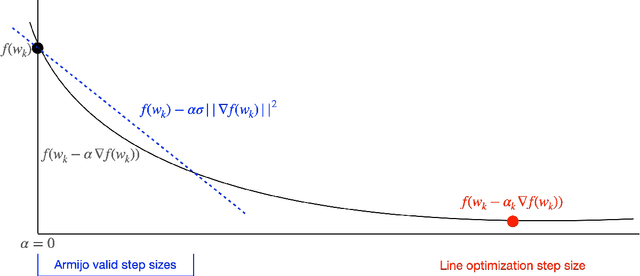
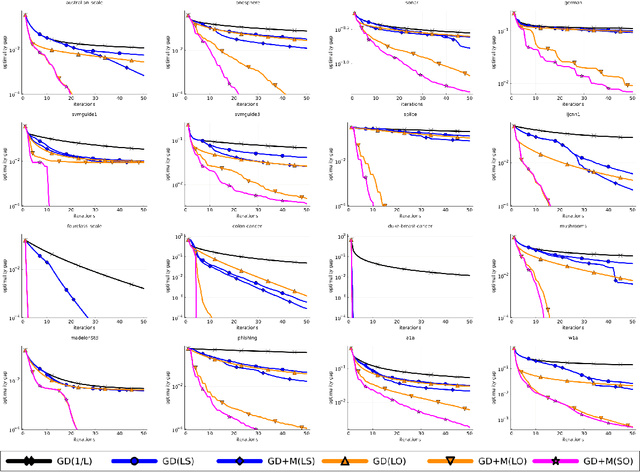
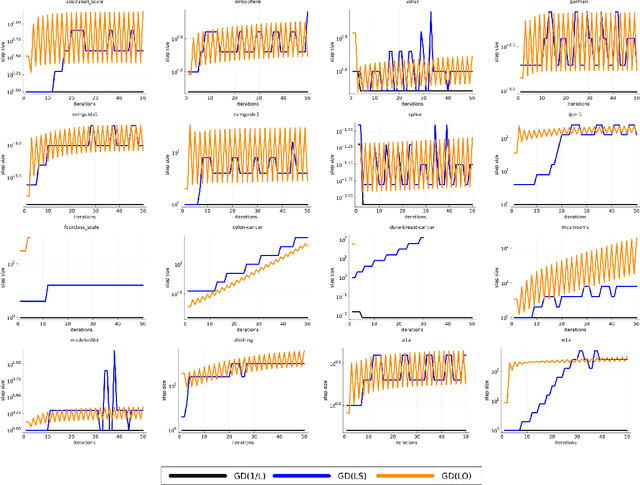
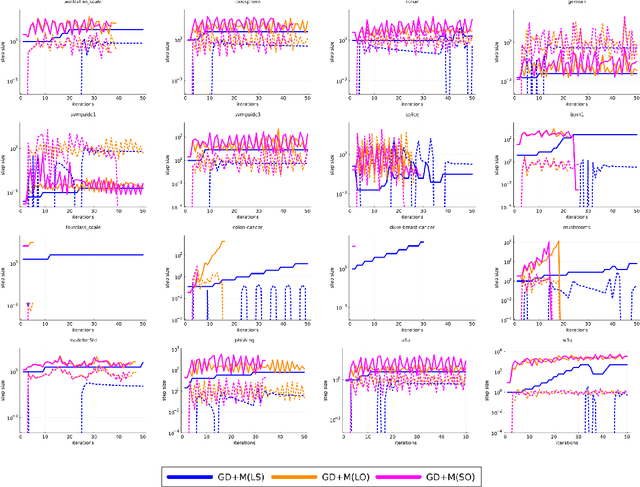
We introduce the class of SO-friendly neural networks, which include several models used in practice including networks with 2 layers of hidden weights where the number of inputs is larger than the number of outputs. SO-friendly networks have the property that performing a precise line search to set the step size on each iteration has the same asymptotic cost during full-batch training as using a fixed learning. Further, for the same cost a planesearch can be used to set both the learning and momentum rate on each step. Even further, SO-friendly networks also allow us to use subspace optimization to set a learning rate and momentum rate for each layer on each iteration. We explore augmenting gradient descent as well as quasi-Newton methods and Adam with line optimization and subspace optimization, and our experiments indicate that this gives fast and reliable ways to train these networks that are insensitive to hyper-parameters.