AgentAda: Skill-Adaptive Data Analytics for Tailored Insight Discovery

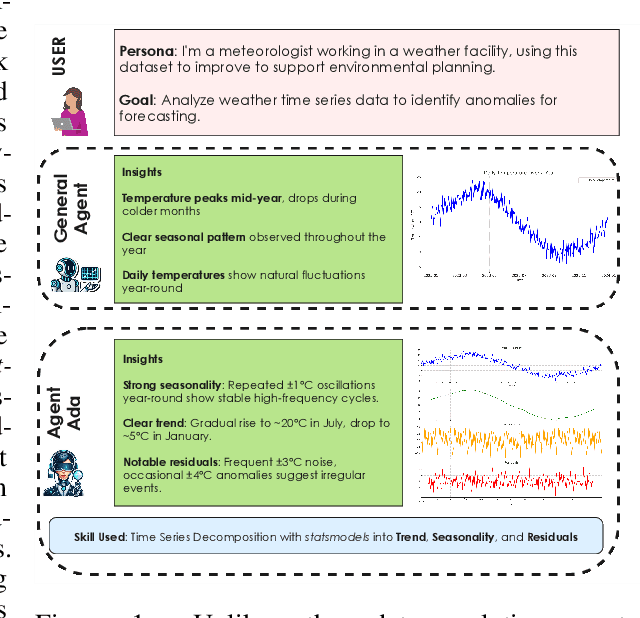
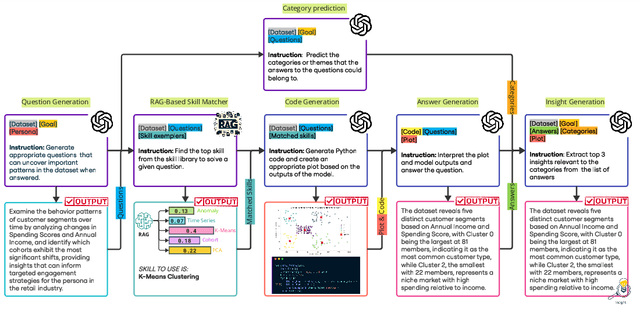
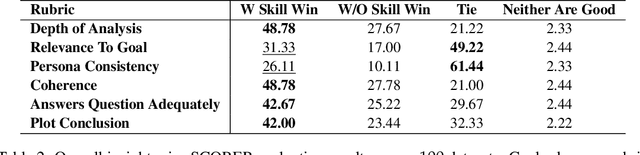
We introduce AgentAda, the first LLM-powered analytics agent that can learn and use new analytics skills to extract more specialized insights. Unlike existing methods that require users to manually decide which data analytics method to apply, AgentAda automatically identifies the skill needed from a library of analytical skills to perform the analysis. This also allows AgentAda to use skills that existing LLMs cannot perform out of the box. The library covers a range of methods, including clustering, predictive modeling, and NLP techniques like BERT, which allow AgentAda to handle complex analytics tasks based on what the user needs. AgentAda's dataset-to-insight extraction strategy consists of three key steps: (I) a question generator to generate queries relevant to the user's goal and persona, (II) a hybrid Retrieval-Augmented Generation (RAG)-based skill matcher to choose the best data analytics skill from the skill library, and (III) a code generator that produces executable code based on the retrieved skill's documentation to extract key patterns. We also introduce KaggleBench, a benchmark of curated notebooks across diverse domains, to evaluate AgentAda's performance. We conducted a human evaluation demonstrating that AgentAda provides more insightful analytics than existing tools, with 48.78% of evaluators preferring its analyses, compared to 27.67% for the unskilled agent. We also propose a novel LLM-as-a-judge approach that we show is aligned with human evaluation as a way to automate insight quality evaluation at larger scale.

BlockLLM: Memory-Efficient Adaptation of LLMs by Selecting and Optimizing the Right Coordinate Blocks

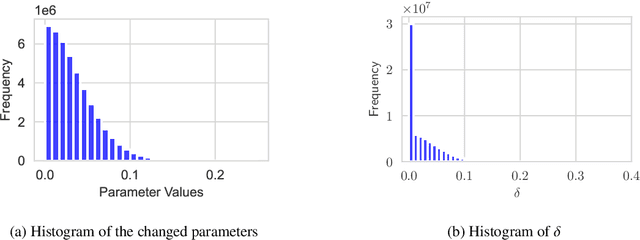
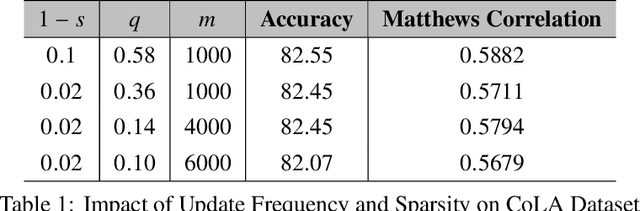
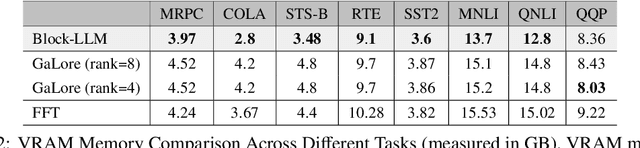
Training large language models (LLMs) for pretraining or adapting to new tasks and domains has become increasingly critical as their applications expand. However, as the model and the data sizes grow, the training process presents significant memory challenges, often requiring a prohibitive amount of GPU memory that may not be readily available. Existing methods such as low-rank adaptation (LoRA) add trainable low-rank matrix factorizations, altering the training dynamics and limiting the model's parameter search to a low-rank subspace. GaLore, a more recent method, employs Gradient Low-Rank Projection to reduce the memory footprint, in the full parameter training setting. However GaLore can only be applied to a subset of the LLM layers that satisfy the "reversibility" property, thus limiting their applicability. In response to these challenges, we introduce BlockLLM, an approach inspired by block coordinate descent. Our method carefully selects and updates a very small subset of the trainable parameters without altering any part of its architecture and training procedure. BlockLLM achieves state-of-the-art performance in both finetuning and pretraining tasks, while reducing the memory footprint of the underlying optimization process. Our experiments demonstrate that fine-tuning with only less than 5% of the parameters, BlockLLM achieves state-of-the-art perplexity scores on the GLUE benchmarks. On Llama model pretrained on C4 dataset, BlockLLM is able to train with significantly less memory than the state-of-the-art, while still maintaining competitive performance.

Analyzing and Improving Greedy 2-Coordinate Updates for Equality-Constrained Optimization via Steepest Descent in the 1-Norm

We consider minimizing a smooth function subject to a summation constraint over its variables. By exploiting a connection between the greedy 2-coordinate update for this problem and equality-constrained steepest descent in the 1-norm, we give a convergence rate for greedy selection under a proximal Polyak-Lojasiewicz assumption that is faster than random selection and independent of the problem dimension $n$. We then consider minimizing with both a summation constraint and bound constraints, as arises in the support vector machine dual problem. Existing greedy rules for this setting either guarantee trivial progress only or require $O(n^2)$ time to compute. We show that bound- and summation-constrained steepest descent in the L1-norm guarantees more progress per iteration than previous rules and can be computed in only $O(n \log n)$ time.