Lower Bounds for Private Estimation of Gaussian Covariance Matrices under All Reasonable Parameter Regimes

We prove lower bounds on the number of samples needed to privately estimate the covariance matrix of a Gaussian distribution. Our bounds match existing upper bounds in the widest known setting of parameters. Our analysis relies on the Stein-Haff identity, an extension of the classical Stein's identity used in previous fingerprinting lemma arguments.

Searching for Optimal Per-Coordinate Step-sizes with Multidimensional Backtracking

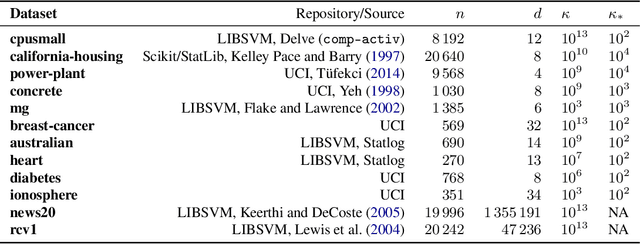
The backtracking line-search is an effective technique to automatically tune the step-size in smooth optimization. It guarantees similar performance to using the theoretically optimal step-size. Many approaches have been developed to instead tune per-coordinate step-sizes, also known as diagonal preconditioners, but none of the existing methods are provably competitive with the optimal per-coordinate stepsizes. We propose multidimensional backtracking, an extension of the backtracking line-search to find good diagonal preconditioners for smooth convex problems. Our key insight is that the gradient with respect to the step-sizes, also known as hypergradients, yields separating hyperplanes that let us search for good preconditioners using cutting-plane methods. As black-box cutting-plane approaches like the ellipsoid method are computationally prohibitive, we develop an efficient algorithm tailored to our setting. Multidimensional backtracking is provably competitive with the best diagonal preconditioner and requires no manual tuning.

Settling the Sample Complexity for Learning Mixtures of Gaussians

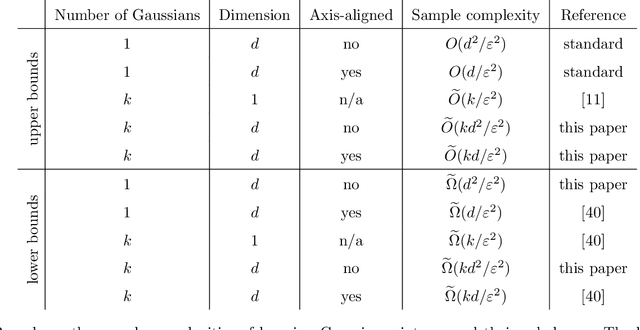
We prove that $\widetilde{\Theta}(k d^2 / \varepsilon^2)$ samples are necessary and sufficient for learning a mixture of $k$ Gaussians in $\mathbf{R}^d$, up to error $\varepsilon$ in total variation distance. This improves both the known upper bound and lower bound for this problem. For mixtures of axis-aligned Gaussians, we show that $\widetilde{O}(k d / \varepsilon^2)$ samples suffice, matching a known lower bound. Moreover, these results hold in an agnostic learning setting as well. The upper bound is based on a novel technique for distribution learning based on a notion of sample compression. Any class of distributions that allows such a sample compression scheme can also be learned with few samples. Moreover, if a class of distributions has such a compression scheme, then so do the classes of products and mixtures of those distributions. The core of our main result is showing that the class of Gaussians in $\mathbf{R}^d$ has an efficient sample compression.

Nearly-tight VC-dimension and pseudodimension bounds for piecewise linear neural networks

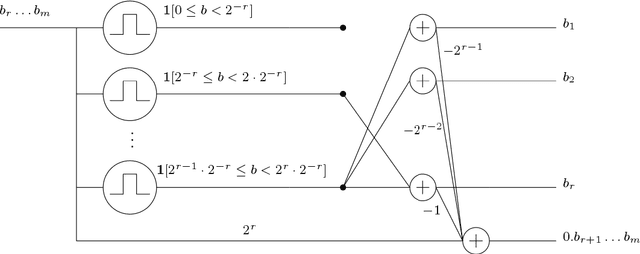
We prove new upper and lower bounds on the VC-dimension of deep neural networks with the ReLU activation function. These bounds are tight for almost the entire range of parameters. Letting $W$ be the number of weights and $L$ be the number of layers, we prove that the VC-dimension is $O(W L \log(W))$, and provide examples with VC-dimension $\Omega( W L \log(W/L) )$. This improves both the previously known upper bounds and lower bounds. In terms of the number $U$ of non-linear units, we prove a tight bound $\Theta(W U)$ on the VC-dimension. All of these bounds generalize to arbitrary piecewise linear activation functions, and also hold for the pseudodimensions of these function classes. Combined with previous results, this gives an intriguing range of dependencies of the VC-dimension on depth for networks with different non-linearities: there is no dependence for piecewise-constant, linear dependence for piecewise-linear, and no more than quadratic dependence for general piecewise-polynomial.