Settling the Sample Complexity for Learning Mixtures of Gaussians
Paper and Code
Feb 16, 2018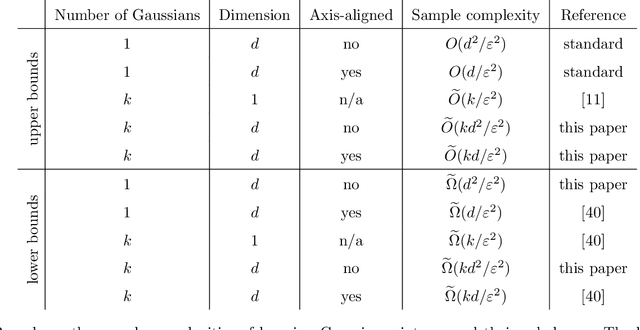
We prove that $\widetilde{\Theta}(k d^2 / \varepsilon^2)$ samples are necessary and sufficient for learning a mixture of $k$ Gaussians in $\mathbf{R}^d$, up to error $\varepsilon$ in total variation distance. This improves both the known upper bound and lower bound for this problem. For mixtures of axis-aligned Gaussians, we show that $\widetilde{O}(k d / \varepsilon^2)$ samples suffice, matching a known lower bound. Moreover, these results hold in an agnostic learning setting as well. The upper bound is based on a novel technique for distribution learning based on a notion of sample compression. Any class of distributions that allows such a sample compression scheme can also be learned with few samples. Moreover, if a class of distributions has such a compression scheme, then so do the classes of products and mixtures of those distributions. The core of our main result is showing that the class of Gaussians in $\mathbf{R}^d$ has an efficient sample compression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge